ЕГЭ по математике, профильный уровень. Задачи на оптимальный выбор

Математика Подготовка к ЕГЭ ЕГЭ по математике

Условие:

В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x² человеко-часов труда, а для добычи у кг никеля в день требуется у² человеко-часов труда.

Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?

Решение

Рассмотрим условия для первой области.

Поскольку алюминий и никель по условию задачи взаимозаменяемы, а рабочие первой области одинаково эффективно добывают и алюминий, и никель, они могут добывать любой из металлов без снижения показателей эффективности.

За сутки ими будет добыто 160 · 5 · 0,1 = 80 кг металла. Это может быть один из металлов, а может быть два металла, но именно в этом количестве.

Рассмотрим условия для второй области.

Пусть во второй области алюминий добывают t рабочих, а никель — 160 − t рабочих. Тогда за сутки они добудут следующее количество:

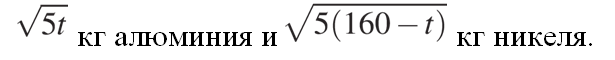
Найдем наибольшее значение функции:

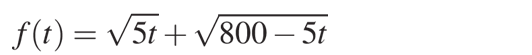
Проведем анализ. Для натуральных t, не больших 160, имеем:

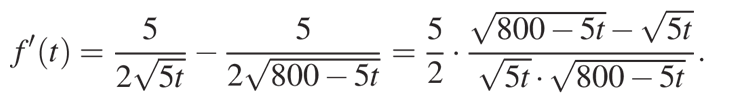
Найдем нули производной:

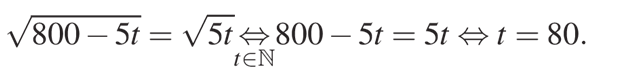
Получается, что при t меньших 80 производная положительна, а при t больших 80 производная отрицательна, поэтому в точке t = 80 функция достигает максимума: fmax=40, равного наибольшему значению функции на исследуемом промежутке.

Делаем вывод, что 80 рабочих второй области следует направить на добычу алюминия и 80 — на добычу никеля. Они добудут 40 кг металла. Совместно рабочие первой и второй области добудут 120 кг металла.

Ответ: 120 кг.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

ЕГЭ по математике, профильный уровень. Задачи на оптимальный выбор

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи