ЕГЭ по математике, базовый уровень. Задачи с показательными уравнениями и неравенствами

Математика Подготовка к ЕГЭ ЕГЭ по математике

Задача №1

Уравнение процесса, в котором участвовал газ, записывается в виде pV^а = const

Где:

p - давление в газе в паскалях

V - объeм газа в кубических метрах

a - положительная константа

При каком наименьшем значении константы «a» уменьшение вдвое раз объeма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?

Решение

Пусть

p₁ и V₁ - начальные,

p₂ и V₂ - конечные

значения объема и давления газа, соответственно.

Задача сводится к решению неравенства:

\(p_2\over p_1 \) ≥ 4

Причем:

\(V_1\over V_2 \) = 2

Запишем:

\(({V_1\over V_2} )^a\) ≥ 4 <=>

<=> 2^a ≥ 4 <=>

<=> a ≥ 2

Ответ: 2.

Задача №2

Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением:

pV^1,4 = const

Где:

p - давление в газе в паскалях

V - объeм газа в литрах

Изначально объeм газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.

Решение

Пусть

p₁ и V₁ - начальные,

p₂ и V₂ - конечные

значения объема и давления газа, соответственно.

Задача сводится к решению неравенства:

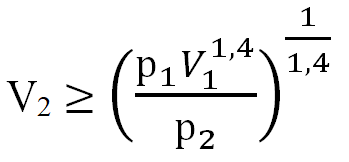
Где:

р₁ = 1 атм.

V₁ = 1,6 л.

р₂ = 128 атм.

Тогда, получаем:

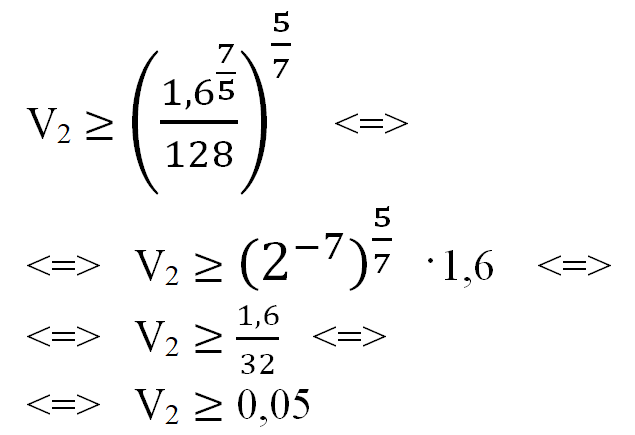
Ответ: 0,05.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Умножения и деление отрицательных чисел

Обновлено: 23 июл 2024

Площади ромба

Обновлено: 29 мар 2025

Формула площади эллипса

Обновлено: 29 дек 2024

Формулы длины дуги

Обновлено: 08 авг 2024

Как найти делитель?

Обновлено: 24 май 2024

Как перевести центнеры в граммы?

Обновлено: 05 ноя 2024

Как по координатам вершин треугольника записать уравнения сторон и уравнение биссектрисы

Обновлено: 03 июн 2024

ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 5)

Обновлено: 30 сен 2024