О платформе 
Премиум математика 
Репетиторы 
Тарифы 
Вход
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 3)
Обновлено: 03 апр 2024
ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 3)
Задача № 1
В треугольнике АВС угол С равен 90° (Рис. 1), CH — высота, BC = 8, BH = 4. Найдите sin A.
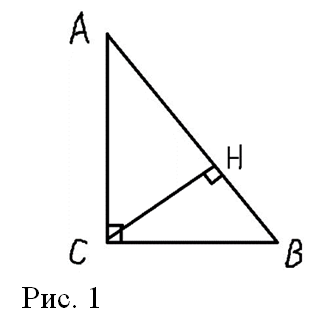
Решение
Рассмотрим углы САВ и НСВ. Эти углы равны по свойству острых углов со взаимно перпендикулярными сторонами.
Поэтому:
\(sinA=sinHCB={HB\over CB}\)
Подставим численные значения:
\(sinA={4\over 8}=0,5\)
Ответ: 0,5
Задача № 2
В треугольнике АВС угол С равен 90° (Рис. 2), CH — высота, BC = 25, BH = 20. Найдите cos A.
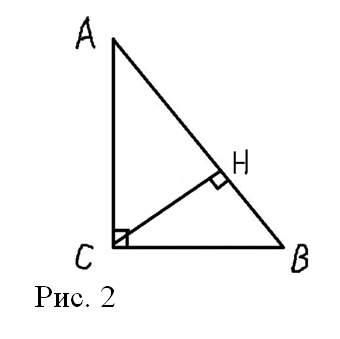
Решение
Рассмотрим углы САВ и НСВ. Эти углы равны по свойству острых углов со взаимно перпендикулярными сторонами.
Поэтому:
\(cosA=cosHCB={HB\over CB}={{\sqrt {CB^2-HB^2} }\over CB}\)
Подставим численные значения:
\(cosA={{\sqrt {25^2-20^2}}\over25}=0,6\)
Ответ: 0,6.
Задача № 3
В треугольнике АВС угол С равен 90° (Рис. 3), CH – высота, , BH = 4. Найдите tg A.
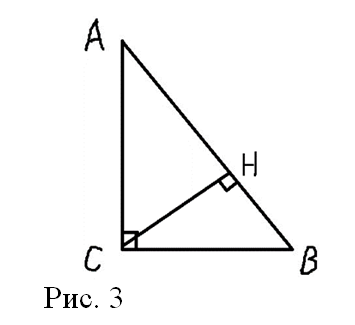
Решение
Рассмотрим углы САВ и НСВ. Эти углы равны по свойству острых углов со взаимно перпендикулярными сторонами.
Поэтому:
\(tgA=tgHCB={BH\over CH}={BH\over \sqrt{CB^2-HB^2 }}\)
Подставим численные значения:
Ответ: 0,5.
Дарим в подарок бесплатный вводный урок!
Репетиторы
![arrow]()
Специализация
![arrow]()
-
![rhombus]()
Репетитор по профильной математике ЕГЭ -
![rhombus]()
Репетитор по химии для подготовки к ЕГЭ -
![rhombus]()
Репетитор по химии для подготовки к ОГЭ -
![rhombus]()
Репетитор по английскому языку для подготовки к ОГЭ -
![rhombus]()
Репетитор по грамматике английского языка -
![rhombus]()
Репетитор для подготовки к ВПР по обществознанию -
![rhombus]()
Репетитор для подготовки к ЕГЭ по обществознанию -
![rhombus]()
Репетитор по географии для подготовки к ЕГЭ -
![rhombus]()
Репетитор по географии для подготовки к ОГЭ -
![rhombus]()
Репетитор Scratch
Похожие статьи
Арифметические действия
Обновлено: 31 дек 2023
Стадии подготовки к экзамену по математике
Обновлено: 03 мар 2024
Вписанный угол окружности
Обновлено: 16 мар 2024
Движение в одном направлении
Обновлено: 08 фев 2024
РУДН: прикладная математика и информатика (очно / заочно)
Обновлено: 11 мар 2024
Планиметрическая задача
Обновлено: 29 май 2024
ЕГЭ по математике, профильный уровень. Окружности и четырехугольники
Обновлено: 05 янв 2024
Знаменитые женщины-математики
Обновлено: 01 мар 2024