С 10 до 22.00 по МСК ежедневно
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 4)
24 фев 2024
ЕГЭ по математике, базовый уровень. Задачи на исследование функций (вариант 4)
Задача №1
Найдите наименьшее значение функции:
у = х3 – х2 – 40х + 3
на отрезке [0; 4]
Решение
Найдем производную заданной функции:
у' = 3х2 - 2х - 40
Найдем нули производной:
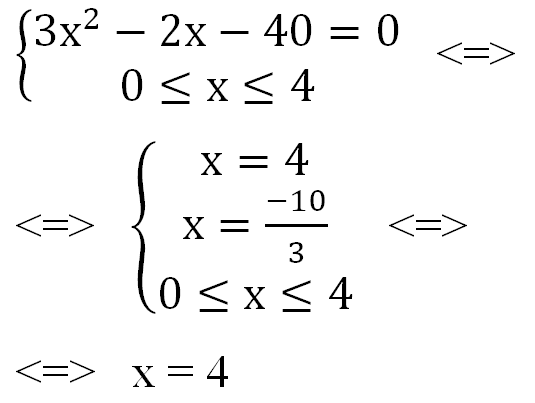
Определим знаки производной функции и изобразим на рисунке (Рис.1) поведение функции:
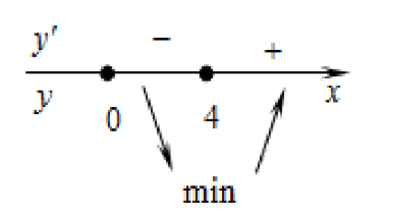
Рис.1
В точке х = 4 заданная функция имеет минимум, являющийся ее наименьшим значением на заданном отрезке. Найдем это наименьшее значение:
у(4) = 64 – 16 – 160 + 3 = -109
Ответ: −109.
Задача №2
Найдите наибольшее значение функции:
у = х3 + 2х2 – 4х + 4
на отрезке [-2; 0]
Решение
Найдем производную заданной функции:
у' = 3х2 + 4х - 4
Из уравнения:
3х2 + 4х – 4 = 0
найдем нули производной:
х1 = -2
х2 =
Определим знаки производной функции и изобразим на рисунке (Рис.2) поведение функции:
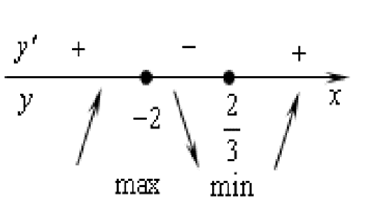
Рис.2
На отрезке [−2; 0] функция убывает, поэтому она достигает своего наибольшего значения в точке x = −2.
Найдем это наибольшее значение:
у(-2) = (-2)3 + 2 · (-2)2 – 4 · (-2) + 4 = 12
Ответ: 12
Дарим в подарок бесплатный вводный урок!
Репетиторы
![arrow]()
Специализация
![arrow]()
-
![rhombus]()
Подготовка к ОГЭ по математике -
![rhombus]()
Репетитор по геометрии -
![rhombus]()
Репетитор по химии для подготовки к ЕГЭ -
![rhombus]()
Репетитор по химии для подготовки к ОГЭ -
![rhombus]()
Репетитор для подготовки к ЕГЭ по физике -
![rhombus]()
Репетитор для подготовки к сочинению ЕГЭ по русскому -
![rhombus]()
Репетитор по английскому языку для подготовки к ЕГЭ -
![rhombus]()
Репетитор по грамматике английского языка -
![rhombus]()
Репетитор по географии для подготовки к ЕГЭ -
![rhombus]()
Программирование Pascal
Похожие статьи
Правила вычитания векторов
24 май 2024
Среднее арифметическое
24 июл 2024
Формула пути
24 май 2024
17 задача профильного ЕГЭ на вклады с платежами равными взносами
24 авг 2024
ЕГЭ по математике, базовый уровень. Задачи на совместную работу (вариант 5)
24 фев 2024
Как выбрать велосипед для школьника
24 июн 2024
Как обустроить комнату для школьника?
24 авг 2024
Как перевести десятичную дробь в обыкновенную: 2 способа
24 авг 2024