Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Векторы
Что такое вектор?
Векторы могут быть графически представлены направленными отрезками. Длина выбирается, согласно некоторому масштабу, а направление направленного отрезка линии представляет направление вектора. Например, если мы обозначим, что \(1\) см - \(5\) км/ч, то \(15\) км/ч ветер с северо-запада будет направленным отрезком \(3\) см, как показано на рисунке снизу.
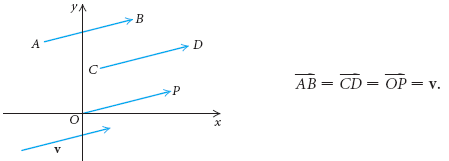
Вектор на плоскости - это направленный отрезок. Два вектора считаются эквивалентны, если они имеют одинаковую величину и направление.
Рассмотрим вектор, взятый из точки \(A\) в точку \(B\). точка \(A\) называется начальной точкой вектора, а точка \(B\) называется конечной точкой. Символьная запись читается как вектор AB. Векторы также обозначаются английскими прописными буквами, такими как \(\overline{u},\overline{v}\) и \(\overline{w}\) или большими буквами \(\overline{AB}, \overline{CD}\)с чертой сверху. Чтобы определить, эквивалентны ли векторы, мы учитываем их величины и направления. Четыре вектора на рисунке сверху \(\overline{AB}, \overline{CD},\overline{OP},\overline{v}\) имеют одинаковую длину и направление. Таким образом, они эквивалентны.
Для равенство векторов используют знак \(=\) .
Для равенство векторов используют знак \(=\) .
Длину вектора обозночают как \(|\overline{AB}|\).
Задача 1. Векторы \(u\), и \(w\) показаны на рисунке ниже. Найти длину векторов:
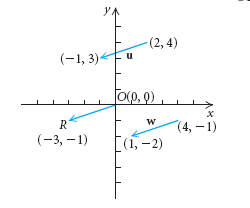
Решение сначала найдем длину каждого вектора, используя формулу расстояния:
- \( |\overline{u}| = \sqrt{[2 - (-1)]^2} + (4 - 3)^2 =\sqrt{9 + 1} = \sqrt{10}\)
- \(|\overline{OR}| = \sqrt{[0 - (-3)]^2} + \sqrt{[0 - (-1)]^2} = \sqrt{9 + 1} = \sqrt{10}\)
- \(|\overline{w}| =\sqrt{(4 - 1)2} +\sqrt{ [-1 - (-2)]^2} = \sqrt{9 + 1} = \sqrt{10}\)
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике -
 Репетитор по геометрии
Репетитор по геометрии -
 Подготовка к ЕГЭ по математике профильный уровень
Подготовка к ЕГЭ по математике профильный уровень -
 Подготовка к итоговому сочинению русский язык
Подготовка к итоговому сочинению русский язык -
 Репетитор по грамматике русского языка
Репетитор по грамматике русского языка -
 Репетитор по грамматике английского языка
Репетитор по грамматике английского языка -
 Подготовка к ЕГЭ по истории
Подготовка к ЕГЭ по истории -
 Репетитор по математике впр
Репетитор по математике впр -
 Репетитор по информатике ОГЭ онлайн
Репетитор по информатике ОГЭ онлайн -
 Репетитор Scratch
Репетитор Scratch


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

