Формулы параболы

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Напомним графиком квадратичной функции является парабола \(y = ax^2 + bx + c\) , где \(a ≠ 0\).

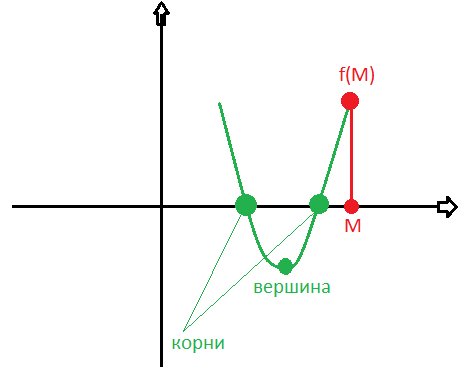
Осью симметрии параболы является линия, которая проходит через центр и через вершину параболы, таким образом, разделив график на две равные части.

Парабола

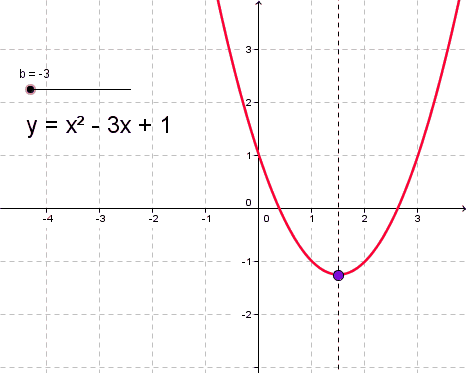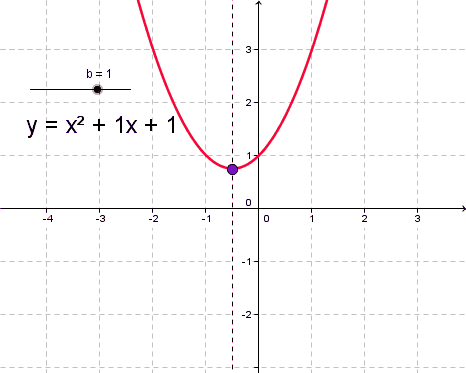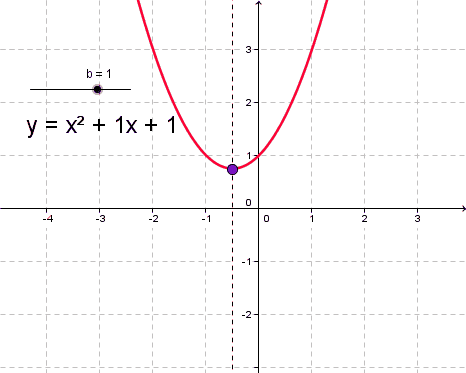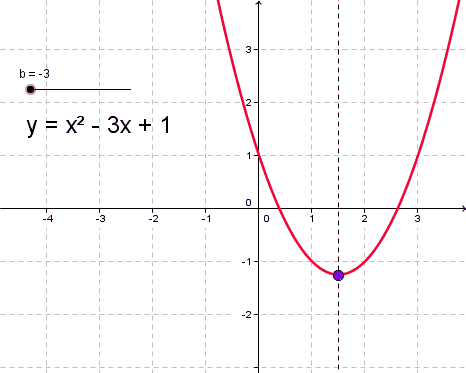
Вершина параболы - это точка, в которой парабола пересекает оси координат и не может идти выше или ниже в координатной плоскости. Это точка, где парабола принимает самый резкий поворот.

Для вычисления вершины параболы используют формулу:

\([{\frac{-b}{2a}; -\frac{b^2-4ac}{4a}}]\)

Дискриминант показывает пересечение ветвей параболы с осями координат:

Парабола

\(D=b^2-4ac\)

\(x_1=\frac{-b+\sqrt{D}}{2a}\) \(x_1=\frac{-b-\sqrt{D}}{2a}\)

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Решение уравнений с одной переменной

Обновлено: 28 фев 2025

Деление и умножение десятичных дробей

Обновлено: 27 июл 2024

Умножение и деление дробей

Обновлено: 29 июн 2024

Эллипс

Обновлено: 23 июл 2024

Типы четырехугольников

Обновлено: 04 авг 2024

Свойства скалярного произведения

Обновлено: 08 июл 2024

Площадь параллелограмма

Обновлено: 30 ноя 2024

Задачи на исследование функций

Обновлено: 02 июн 2024