Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Задача по планиметрии
Условие:
Окружность с центром О1 касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O2 касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.
а) Докажите, что прямая О1О2 параллельна основаниям трапеции АВСD.
б) Найдите О1О2.
Решение
а) Построим чертеж, согласно условию задачи (Рис.1). Из рисунка видно, что, согласно построению, точка О1 как центр окружности будет равноудалена от прямых AD и ВС на расстояние, равное радиусу. А это значит, что точка О1 лежит на средней линии трапеции АВСD. Точно так же, точка О2 лежит на средней линии трапеции АВСD. Так как эти точки принадлежат средней линии трапеции, то прямая О1О2 будет параллельна основаниям трапеции АВСD. Что и требовалось доказать.
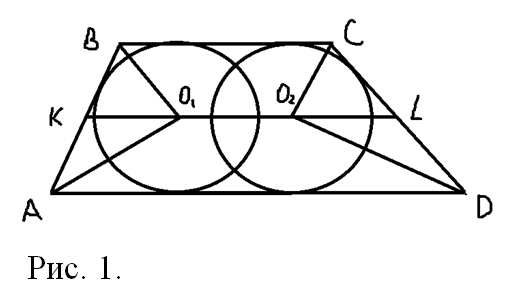
б) Введем дополнительные обозначения.
Пусть точка К — середина стороны АВ, а точка L — середина стороны CD.
Точка О1 равноудалена от прямых АВ, ВС и AD на расстояние радиуса, поэтому лучи АО1 и ВО1 являются биссектрисами углов DAB и ABC соответственно. Поэтому,
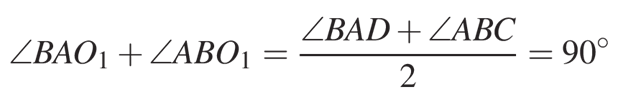
то есть, получается, что: ![]()

Так как точка К является серединой отрезка АВ, то отрезок КО1 является медианой, проведенной к гипотенузе АВ прямоугольного треугольника АО1В.
Аналогично треугольник СО2D тоже прямоугольный, а отрезок LO2 является медианой, проведенной к его гипотенузе CD. Соответственно, точки К, О1, О2 и L лежат на средней линии трапеции АВСD. Значит, мы можем записать и вычислить:
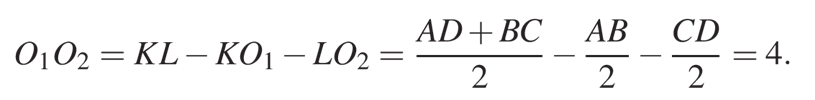
Ответ: 4.
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор по олимпиадной математике
Репетитор по олимпиадной математике -
 Репетитор для подготовки к ОГЭ по химии
Репетитор для подготовки к ОГЭ по химии -
 Репетитор для подготовки к ЕГЭ по физике
Репетитор для подготовки к ЕГЭ по физике -
 Репетитор для подготовки к ОГЭ по физике
Репетитор для подготовки к ОГЭ по физике -
 Репетитор для подготовки к ОГЭ по русскому языку
Репетитор для подготовки к ОГЭ по русскому языку -
 Репетитор по грамматике русского языка
Репетитор по грамматике русского языка -
 Репетитор по английскому для взрослых
Репетитор по английскому для взрослых -
 Репетитор по обществознанию ОГЭ
Репетитор по обществознанию ОГЭ -
 Репетитор для подготовки к ОГЭ по географии
Репетитор для подготовки к ОГЭ по географии -
 Репетитор по информатике ОГЭ онлайн
Репетитор по информатике ОГЭ онлайн


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

