Степенные ряды

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Определение 1. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают: u1(x)+u2(x)+…+un(x)+… .

Определение 2. Если при x=x0 функциональный ряд сходится, то x0 называется точкой сходимости функционального ряда.

Определение 3. Множество всех точек сходимости функционального ряда называется его областью сходимости.

Очевидно, что в области сходимости функционального ряда его сумма является функцией от x. Будем обозначать её S(x).

Определение 4. Степенным рядом называется функциональный ряд вида

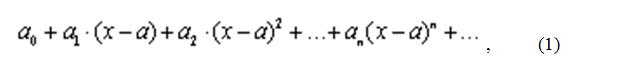
где a, a0, a1, a2, …, an, … – некоторые числа, называемые коэффициентами степенного ряда.

Теорема 1. (О структуре области сходимости степенного ряда)

Областью сходимости степенного ряда (1) является интервал (a-R;a+R), к которому в зависимости от конкретных случаев могут быть присоединены точки a-R и a+R, где R=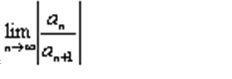

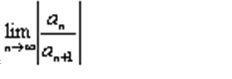(если этот предел существует). В каждой точке интервала (a-R;a+R) ряд сходится абсолютно.

Доказательство. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда:

|a0|+|a1|.|x-a|+|a2|.|x-a|2+…+|an|.|x-a|n+… (2)

Применим к ряду (2) признак Даламбера

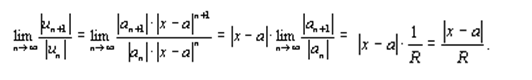
Возможны три случая:

1. Если \({|x-a|}\over R\) < 1 или |x-a|<R или xЄ(a-R;a+R), то ряд (2) сходится, но тогда по достаточному признаку сходимости знакопеременного ряда сходится и ряд (1), причём абсолютно.

2. Если \({|x-a|}\over R\)> 1, то ряд (2) расходится. В этом случае

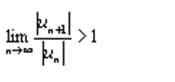, то есть при достаточно больших n|un+1|>|un|,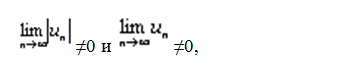

следовательно, ряд (1) расходится по следствию из необходимого признака сходимости. Теорема доказана.

Определение 14. Интервал (a-R;a+R), называется интервалом сходимости степенного ряда, а половина его длины R называется радиусом сходимости степенного ряда.

Замечание. Любой степенной ряд (1) сходится при x=a. Если других точек сходимости у ряда (1) нет, то считают, что R=0. Если степенной ряд (1) сходится во всех точках числовой прямой, то считают, что R=∞.

Свойства степенных рядов

Отметим здесь без доказательства три важных свойства степенных рядов:

1. Сумма S(x) степенного ряда

S(x)=a0+a1(x-a)+a2(x-a)2+…+an(x-a)n+… (1)

является непрерывной функцией в каждой точке интервала сходимости (a-R;a+R).

2. Ряд

φ(x)=a1+2a2(x-a)+…+nan(x-a)n-1+…, (3)

полученный почленным дифференцированием ряда (1), является степенным рядом с тем же, что и ряд (1), интервалом сходимости (a-R;a+R).

Сумма ряда (3) φ(x)=S'(x).

Замечание. Ряд (3) также можно почленно дифференцировать и сумма полученного после этого ряда равна φ' (x)=S''(x) и так далее. Таким образом, сумма S(x) ряда (24) является бесконечно дифференцируемой функцией в интервале сходимости (a-R; a+R). Сумма ряда, полученного из ряда (1) n-кратным дифференцированием равна \(S^n\)(x). Область сходимости степенного ряда при дифференцируемости не меняется.

3. Пусть числа a и β принадлежат интервалу сходимости (a-R; a+R) ряда (1). Тогда имеет место равенство

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

Степенные ряды

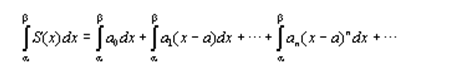
Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи