Сложение и вычитание отрицательных чисел

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Правила и примеры с отрицательными числами
Часто задаваемые вопросы:

24 сен 2024

Сложение и вычитание отрицательных чисел

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны - положительные.

Ноль — это нейтральный элемент относительно сложения целых чисел.

В основном в этой статье мы будем изучать действия (сложение и вычитание) с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании отрицательных чисел:

Правила для знаков при сложении и вычитании

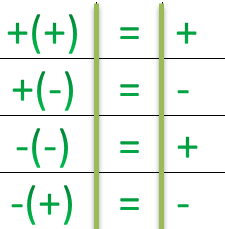
Правила и примеры с отрицательными числами

Чтобы понимать, как решать примеры с отрицательными числами, нужно помнить о некоторых правилах:

Как сложить два отрицательных числа? Для этого надо сложить два числа и поставить знак минус.

\((-2)+(-3)=-5\)

Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

\((-8)+4=4-8=-4\)

\(9+(-4)=9-4=5\)

Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:

\(-9+9=0\) \(7,1+(-7,1)=0\)

Как вычитать отрицательные числа? При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

\((-7)-(-6)=(-7)+6=(-1)\)

Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

\(7-9=-2\) так как \(9>7\)

Всегда помним: минус на минус дает плюс:

\(7-(-9)=7+9=16\)

Задача 1. Вычислите:

\(4+(-5)\)
\(-36+15\)
\((-17)+(-45)\)
\(-9+(-1)\)

Решение:

\(4+(-5)=4-5=-1\)
\(-36+15=-21\)
\((-17)+(-45)\) \(=-17-45=-62\)
\(-9+(-1)=-9-1=-10\)

Задача 2. Вычислите:

\(3-(-6)\)
\(-16-35\)
\(-27-(-5)\)
\(-94-(-61)\)

Решение:

\(3-(-6)=3+6=9\)
\(-16-35=-51\)
\(-27-(-5)=-27+5=-22\)
\(-94-(-61)=-94+61=-33\)

Часто задаваемые вопросы:

✅ Как можно представить сложение и вычитание отрицательных чисел на числовой прямой?

↪ Представьте каждое число как точку на числовой прямой. Сложение отрицательного числа эквивалентно движению влево на числовой прямой, а вычитание отрицательного числа эквивалентно движению вправо.

✅ Что произойдет, если сложить положительное и отрицательное число?

↪ Если абсолютное значение отрицательного числа больше, результат будет отрицательным, и наоборот. Например: 5+(−3)=25+(−3)=2, а 3+(−5)=−23+(−5)=−2

✅ Почему важно понимать сложение и вычитание отрицательных чисел?

↪ Основы арифметики с отрицательными числами лежат в основе многих математических и физических концепций, и умение правильно работать с ними является ключевым для понимания более сложных тем.

Предыдущая статья