Правильный шестиугольник

 

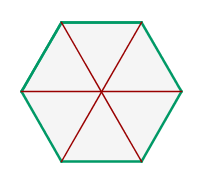
• Правильный шестиугольник имеет \(6\) сторон, \(6\) углов и 6 вершин.
• Сумма внутренних углов шестиугольника \(-(6 − 2) · 180° = 720°\).
• Внутренний угол правильного шестиугольника равен \(720º / 6 = 120º\).
• Центральный угол правильного шестиугольника меры: \(360 : 6 = 60º\).
• Количество диагоналей \(- 6 · (6 − 3) : 2 = 9\).

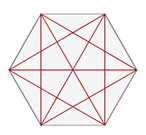
• Апофема правильного шестиугольника:

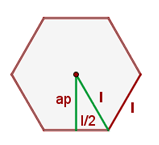
Свойства правильного шестиугольника

Вот некоторые свойства правильного шестиугольника:

1. Равные стороны: Все стороны правильного шестиугольника имеют одинаковую длину. Это означает, что каждая сторона равна другим сторонам в шестиугольнике.

2. Равные углы: Углы в правильном шестиугольнике равны между собой. Каждый угол равен 120 градусам.

3. Сумма углов: Сумма всех углов в правильном шестиугольнике равна 720 градусам. Это можно получить, умножив число углов (6) на величину каждого угла (120 градусов).

4. Центральная симметрия: У правильного шестиугольника есть центр симметрии, что означает, что при вращении шестиугольника вокруг этого центра на угол 60 градусов он будет выглядеть так же, как и до вращения.

5. Радиус окружности: В правильном шестиугольнике можно описать окружность, в которую все вершины шестиугольника попадают на окружность. Радиус этой окружности может быть найден с использованием формулы: радиус = сторона / (√3), где сторона - длина стороны шестиугольника.

6. Площадь: Площадь правильного шестиугольника может быть вычислена с помощью формулы: площадь = (3√3/2) * сторона^2, где сторона - длина стороны шестиугольника.

Эти свойства помогают определить и описать основные характеристики и свойства правильного шестиугольника.

Часто задаваемые вопросы