Площадь поверхности пирамиды

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Площадь поверхности пирамиды

Геометрия является одной из увлекательных областей математики, и одной из ее фундаментальных концепций является площадь поверхности пирамиды. В этой статье мы погрузимся в мир пирамид и изучим, что такое площадь пирамиды и как ее можно вычислить.

Площадь поверхности пирамиды

Найти площадь поверхности пирамиды может быть немного сложнее, если пирамида неправильная, так как треугольные грани будут разными. В таком случае площадь каждой грани пирамиды, включая основание должны быть найдены отдельно, и их значения суммируются, чтобы получить общую площадь.

Если пирамида является правильной пирамидой, жизнь несколько проще. Общая площадь поверхности вычисляется как:

\(S= S_{осн} + \frac{1}{2} pl\)

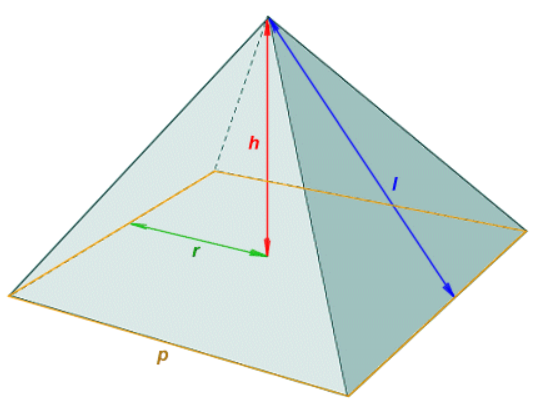
где \(Sосн\) - площадь основания, \(p\) - длина периметра основания, а \(l\) - наклонная высота пирамиды см. рисунок ниже. Обратите внимание, что Наклонная высота \(l\) правильной пирамиды может быть рассчитана по следующей формуле:

\(l = \sqrt{h^2+r^2} \)

где \(h\) - высота пирамиды, а \(r\) - длина основания пирамиды, т. е. длина радиуса вписанной окружности основания, которая также является расстоянием между геометрическим центром основания и центром одной из его сторон.

Объем пирамиды

Объем правильной \(V\) пирамиды, независимо от формы основания, рассчитывается как одна треть от своего основания на высоты то же самое верно и для конуса.

\(V = \frac{1}{3} Sh\)

где \(S\) - площадь основания, а \(h\)- высота пирамиды (перпендикулярное расстояние от основания пирамиды до ее вершины).

Часто задаваемые вопросы:

Часто задаваемые вопросы

Что такое площадь поверхности пирамиды?

Площадь поверхности пирамиды - это сумма площадей всех ее боковых поверхностей плюс площадь ее основания. Она представляет собой меру общей площади поверхности пирамиды.

Как найти площадь поверхности пирамиды, если известны ее боковые грани и основание?

Чтобы найти площадь поверхности пирамиды, нужно сначала вычислить площади всех ее боковых граней, а затем сложить их вместе. Затем добавьте площадь основания пирамиды. Формулу можно записать так: Площадь поверхности пирамиды = Сумма площадей боковых граней + Площадь основания.

Как найти площадь поверхности пирамиды, если известны ее высота и периметр основания?

Если известны высота пирамиды и периметр ее основания, то можно использовать формулу для нахождения площади поверхности. Сначала нужно найти площадь основания, затем умножить ее на половину периметра основания и сложить с площадью всех боковых граней. Формула будет выглядеть так: Площадь поверхности пирамиды = Площадь основания + (1/2) * Периметр основания * Высота.

Предыдущая статья