img
О платформе Новое Премиум математика Репетиторы Тарифы
Записаться на урок

Дарим первый урок с репетитором бесплатно

Оставьте заявку и получите первый урок в подарок

bg bg gift

Как решать типовые задачи на кривые второго порядка

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 13 май 2024

Как решать типовые задачи на кривые второго порядка

 
Найти центр и радиус окружности, заданной уравнением  
 
\(x^2+2y^2+x+3y-1=0\)
 
Решение
 
Приведем исходное уравнение к виду: выделим полные квадраты по x и y, для этого разобьем свободный член на элементы:
 
 
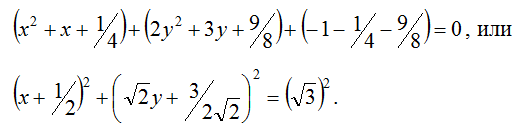
Согласно уравнению получаем
 
 
 
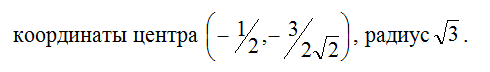
Найти координаты фокусов и эксцентриситет эллипса, описываемого уравнением
 
 \(x^2+9y^2=21\).
 
Решение
 
Приведем уравнение к виду: перепишем в виде:
 
 
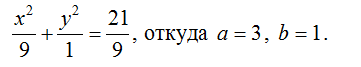
Определяем расстояние фокусов от центра:
 
 
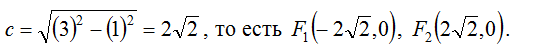
Эксцентриситет данного эллипса определяем по формуле: 
 
 
 
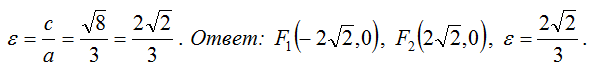
Написать уравнение гиперболы, если ее фокусы находятся в точках F1(-2;0), F2(2;0), а длина ее действительной оси равна 1.
 
Решение
 
Для записи уравнения гиперболы в виде необходимо знать величины a и b. Величина a=1 по условию задачи (длина вещественной оси). Определим величину b.
 
Из условия задачи можно определить величину c. Это первая координата фокуса, то есть c=2.
 
По формуле \(b^2=c^2-a^2\) определяем величину b: 
 
 
Подставляем в уравнение, получаем:
 
Предыдущая статья img Следующая статья img

Дарим в подарок бесплатный вводный урок!

line gift
Репетиторы arrow
Специализация arrow

Похожие статьи

img

Как перевести центнеры в килограммы?

Обновлено: 08 дек 2023

 img

Признак делимости на 19

Обновлено: 09 авг 2024

 img

Финансовый Университет при Правительстве: Информационная Безопасность

Обновлено: 01 янв 2024

 img

Нахождение числа по его части

Обновлено: 28 ноя 2023

 img

Хитрости для написания сочинений по русскому языку и литературе

Обновлено: 06 янв 2024

 img

Изобретения древности, которыми мы пользуемся сегодня

Обновлено: 09 дек 2023

 img

Почему ребенок ест несъедобное и что с этим делать?

Обновлено: 22 фев 2024

 img

Как перевести минуты в секунды

Обновлено: 26 дек 2023