Как решать показательные уравнения

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Свойства и алгоритм решения показательных уравнений
Пример решения показательных уравнений
Часто задаваемые вопросы:

Обновлено: 05 июн 2024

Как решать показательные уравнения

Мы уже неоднократно писали о том, как решать показательные уравнения. Вопрос всегда сводится к умению применять алгоритм. Давайте еще раз повторим основные теоретические положения этой важной темы.

Если в уравнении неизвестное содержится в показателе степени, то такое уравнение называется показательным. Простейшее показательное уравнение имеет вид: а^х = а^b, где а>0, а≠1, х - неизвестное.

Основные свойства степеней, при помощи которых преобразуются показательные уравнения: а>0, b>0.

a⁰ = 1, a¹= а.
a^-n = 1/ aⁿ
aⁿ × a^m = a^n+m
aⁿ/a^m = a^n-m
(aⁿ)^m = a^nm
(ab)ⁿ = aⁿ×bⁿ
(a/b)ⁿ = aⁿ/bⁿ.

При решении показательных уравнений пользуются также следующими свойствами показательной функции: y = a^x, a > 0, a≠1:

ax>0, при всех a>0 и xϵR;

\(a^{x1}=a^{x2}\) ⇔ x1=x2.

Для представления числа в виде степени используют:

a > 0, a≠1, b > 0.

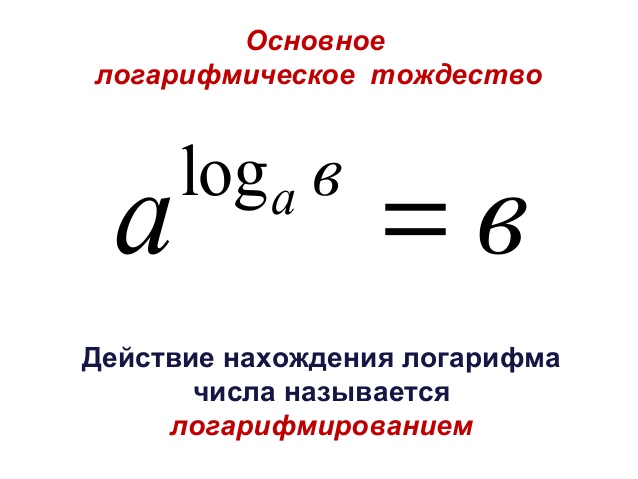
Свойства и алгоритм решения показательных уравнений

Решение уравнений вида а^f⁽^x⁾=a^q⁽^x⁾ сводится к решению уравнения f(x)=q(x). Иногда в таких уравнениях требуется привести обе части к одинаковому основанию степени, как правило, это разные степени одного основания.
Решение уравнений вида а^f⁽^x⁾=b. Для решения используем логарифмирование по основанию а, т.е. решаем уравнение f(x)=log_a^b.
Уравнения, решаемые с помощью вынесения за скобки общего множителя.
Уравнения, решаемые с помощью замены переменной.
Уравнения, содержащие степени с двумя различными (не сводящимися друг к другу) основаниями, a^f⁽^x⁾=b^f⁽^x⁾. Решением является решения уравнения f(x)=0.
Уравнения, однородные относительно a^x и b^x.

Пример решения показательных уравнений

Задание №13.

Условие:

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие промежутку

Решение:

а) Если внимательно посмотреть на исходное уравнение:

то можно заметить, что не только показатели степени одинаковые, но и основания степени можно унифицировать, представив «9» как «3 в квадрате». Это позволит нам сделать замену переменной.

Пусть тогда уравнение мы запишем в виде

Соответственно, у нас получилось квадратное уравнение относительно переменной «t». Решая это уравнение через Дискриминант, получим два корня:

или

Далее делаем обратную замену:

При получим: откуда (так как «1» в правой части, это «3» в «нулевой степени»)

При получим: откуда

Здесь мы сначала используем свойство степени и в левой части «3» в степени «х» разделим на «3» в «первой степени, затем разделим обе части уравнения на три и используем определение логарифма числа.

б) Определим, принадлежат ли полученные корни заданному промежутку.

Корень не принадлежит промежутку , так как концы отрезка в данном случае не входят в промежуток, что обозначено круглыми скобками.

Теперь посмотрим на второй корень. Поскольку и то получается, что корень принадлежит данному промежутку

Ответ: а) б)

Успехов!

Автор - Дмитрий Айстраханов

Часто задаваемые вопросы:

✅ Что такое показательные уравнения?

↪ Показательные уравнения - это уравнения, в которых неизвестные значения находятся в показателях степени. Обычно имеют вид \(a^x = b\), где "a" и "b" - известные числа, а "x" - неизвестное.

✅ Как решить показательное уравнение с одинаковыми основаниями?

↪ Если \(a^x = b\), и "a" возводится в степень "x", чтобы получить "b", тогда \(x = logₐ(b)\). Используйте логарифм с основанием "a", чтобы найти значение "x".

✅ Как решить показательное уравнение с переменным в показателе?

↪ Решайте уравнение, используя свойства логарифмов. Если \(a^x = b\), где "a" - константа, а "x" - переменная, тогда x = logₐ(b). Важно учитывать ограничения области определения, чтобы исключить недопустимые значения.

Предыдущая статья