Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Решаем текстовые задачи
Задача №1
В городе N каждый десятый преподаватель информатики работает также преподавателем математики, а каждый двадцатый преподаватель математики работает также преподавателем информатики. Всего в городе N работают 580 преподавателей. Все преподаватели, которые совмещают должности преподавателей математики и информатики, получают премию.
Выберите утверждения, которые верны при данных условиях.
- Число преподавателей информатики не больше, чем число преподавателей математики.
- Число преподавателей математики меньше, чем число преподавателей информатики.
- Если преподаватель Иван Олегович получает премию, то он преподаёт и математику, и информатику.
- Если в школе №1 города N работает десять преподавателей информатики, то по крайней мере один из них получает премию.
Решение
1. В условии сказано, что в городе 580 преподавателей. Возьмем преподавателей информатики за «х», а преподавателей математики за «у». Тогда сможем записать:
х + у = 580
Отсюда:
Преподавателей математики:
у = 580 – х
Совмещают информатику с математикой каждый десятый, это 10%, или «0,1 х» от общего числа преподавателей.
Совмещают математику с информатикой каждый двадцатый, это 5%, или «0,05 · х» от общего числа преподавателей.
Возьмем граничные условия. Преподавателей математики в городе должно быть не менее 20 человек, тогда совмещать с информатикой сможет хотя бы один преподаватель. Тогда преподавателей информатики будет не более:
580 – 20 = 560
И если совмещают информатику с математикой каждый десятый, это 10%, или «0,1· х» от общего числа преподавателей. Получим:
0,1 · 560 = 56 человек
56 > 20
Первое утверждение неверно.
2. Наименьшее возможное число преподавателей математики мы определили в первом пункте. Наибольшее число преподавателей математики может быть равно:
580 – 20 = 560
Так как это наибольшее число из ряда от 20 до 580, которое делится на 20 без остатка, с учетом условия, есть еще некоторое количество преподавателей информатики, число которых должно быть не меньше 10. Тогда хотя бы один из преподавателей совмещает информатику с математикой.
Наименьшее возможное число преподавателей информатики равно:
580 – 20 = 560
Из первого пункта число преподавателей математики также 20.
20 = 20
Второе утверждение неверно.
3. Поскольку в условии задачи не сказано, что еще кто-то кроме тех, кто совмещает должности преподавателей математики и информатики, получают премию, то заключаем, что если Иван Олегович получает премию, то он преподаёт и математику, и информатику.
Третье утверждение верно.
4. Исходя из условия задачи, что каждый десятый преподаватель информатики работает также преподавателем математики, и учитывая, что в школе №1 работает десять преподавателей информатики, по крайней мере один из них получает премию.
Четвертое утверждение верно.
Ответ: 34
Задача № 2
Рабочие прокладывают тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.
Решение
Пусть рабочие в первый день проложили «а1» метров тоннеля, во второй — «а2», в последний — «а10» метров тоннеля.
Длина тоннеля может быть найдена по формуле:
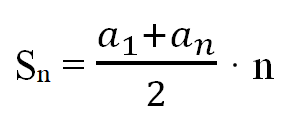
Если работа была выполнена за 10 дней, то получаем, что в последний день рабочие проложили:
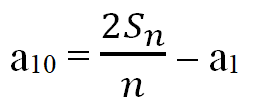
Подставим числовые значения:
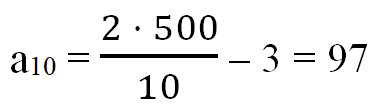
Таким образом, рабочие в последний день проложили 97 метров тоннеля.
Ответ: 97.
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор по олимпиадной математике
Репетитор по олимпиадной математике -
 Репетитор по геометрии
Репетитор по геометрии -
 Подготовка к ЕГЭ по математике профильный уровень
Подготовка к ЕГЭ по математике профильный уровень -
 Репетитор по грамматике русского языка
Репетитор по грамматике русского языка -
 Подготовка к олимпиадам по английскому языку
Подготовка к олимпиадам по английскому языку -
 Репетитор по грамматике английского языка
Репетитор по грамматике английского языка -
 Подготовка к ВПР по русскому
Подготовка к ВПР по русскому -
 Подготовка к ЕГЭ по биологии онлайн
Подготовка к ЕГЭ по биологии онлайн -
 Онлайн репетитор ОГЭ по биологии
Онлайн репетитор ОГЭ по биологии -
 Репетитор по информатике ОГЭ онлайн
Репетитор по информатике ОГЭ онлайн


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

