Решение задач по геометрии синус и косинус угла

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Многие ученики путаются в решении задач используя синус и косинус угла, мы подробно разберём решение таких задач, ведь если разобраться и верно нарисовать рисунок, то это не так уж и сложно. В этой статье вместе с myalfaschool.ru мы научимся решать такие задачи, также ты можешь записаться на бесплатный пробный урок здесь.

Задача 1: \(10\)-метровая лестница опирается на здание таким образом, что угол подъема от земли до здания составляет \(30˚\) градусов. Найдите расстояние от вершины лестницы до земли, кроме того, найдите расстояние от здания до подножья лестницы.

Решение.

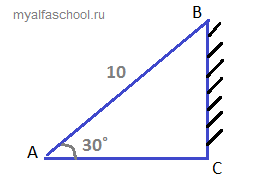
\(AB-\)длина лестница, \(BC-\)расстояние от вершины лестницы до земли, \(AC-\)расстояние от здания до подножья лестницы. Угол \(∠BCA\) равен \(90˚\).

1. Рассмотрим синус угла \(∠BAC\) и найдем \(BC-\) :

\(sin30=\frac{BC}{AB}\)

\(\frac{1}{2}=\frac{BC}{10}-->1*10/2=5-->BC=5\)

2. Далее рассмотрим косинус угла \(∠BAC\) и найдем \(AC:\)

\(cos30=\frac{AC}{AB}\)

\(\frac{\sqrt{3}}{2}=\frac{AC}{10}-->\sqrt{3}*10/2=5-->AC=5\sqrt{3}\)

Ответ: \(BC=5\) м, \(AC=5\sqrt{3}\) м.

Задача 2. Смотритель маяка видит корабль под углом 60˚ . Найдите расстояние от верха маяка до коробля и от низа маяка до корабля, если высота маяка 50 м.

Решение.

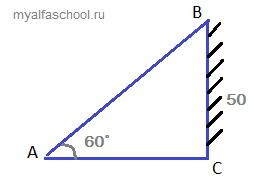
\(AB-\)высота маяка, \(BC-\)расстояние от верха маяка до коробля, \(AC-\) расстояние от низа маяка до корабля. Угол \(∠BCA\) равен \(90˚\).

1. Рассморим синус угла \(∠BAC\) и найдем \(AB\):

\(sin60=\frac{BC}{AB}\)

\(\frac{\sqrt{3}}{2}=\frac{50}{AB}-->2*50/\sqrt{3}=10/1,73=57,8-->AB≈57,8\)

2. Рассморим косинус угла \(∠BAC\) и найдем \(AC\) :

\(cos60=\frac{AC}{AB}\)

\(\frac{1}{2}=\frac{AC}{57,8}-->1*57,8/2=28,9-->AC≈28,9\)

Ответ: \(AB≈57,8\) м, \(AC≈28,9 \) м.

Задача 3. Скалолаз поднимается на 15-градусный уклон у подножья горы. Если он поднимается с постоянной скоростью 3 м в час, то на какой высоте он будет через 5 часов?

Решение.

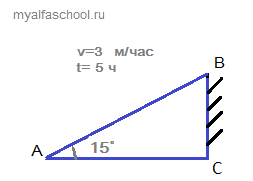
1. Вычислим расстояние \(AB\) через \(5\) часов: \(5*3=15\) м под уклоном \(15˚\).
2. \(AB-15\) м , угол \(∠BAC\) = \(15˚\). Рассмотрим синус угла \(∠BAC\):

\(sin(15)=\frac{BC}{AB}\)

\(0,65=\frac{BC}{15}--> BC = 9,75\)

Ответ: \(9,75 \) м.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

Решение задач по геометрии синус и косинус угла

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи