Углы правильного многоугольника. Формулы

Углы правильного многоугольника делятся на:

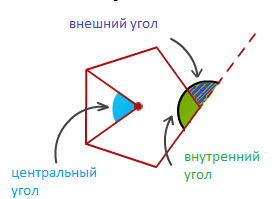
Свойства углов правильного многоугольника

Сумма внутреннего и внешнего угла равна \(180°\).

Сумма внутренних углов правильного многоугольника с \(n\) сторонами равна:

\((n - 2)180°\)

Для нахождения внутреннего угла используют формулу:

\(\alpha = \frac{{{{180}^o}(n - 2)}}{n}\)

\(n\)- число сторон

Для нахождения внешнего угла используют формулу:

\(\varphi = \frac{{{{360}^o}}}{n}\)

\(n\)- число сторон

Для нахождения центрального угла используют формулу:

\(\beta = \frac{{{{360}^o}}}{n}\)

\(n\)- число сторон

Как найти сумму всех углов правильного многоугольника?

Сумма всех углов правильного многоугольника равна 180° * (n - 2), где n - количество сторон многоугольника.

Как найти число диагоналей в правильном многоугольнике?

Число диагоналей в правильном многоугольнике можно найти по формуле: Диагонали = (n * (n - 3)) / 2, где n - количество сторон многоугольника.

Площади ромба

Обновлено: 29 мар 2025

Центральный угол окружности

Обновлено: 12 июл 2025

Вычитание в столбик

Обновлено: 25 мар 2025

Прямая пропорциональная зависимость

Обновлено: 06 май 2025

Как округлить число до тысячных?

Обновлено: 11 май 2025

ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 9)

Обновлено: 07 янв 2025

Степенные ряды

Обновлено: 04 июн 2025

Преобразование иррациональных выражений

Обновлено: 05 май 2025