Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Длина окружности и площадь круга
В нашей повседневной жизни мы часто сталкиваемся с геометрическими фигурами, такими как окружности и круги. Кроме того, эти фигуры имеют свои особенности, которые можно изучить, чтобы лучше понять их свойства и использование. Давайте рассмотрим два основных аспекта окружностей и кругов: длину окружности и площадь круга.
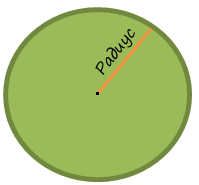
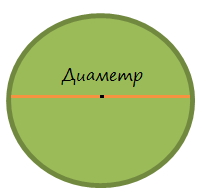
Длина окружности круга
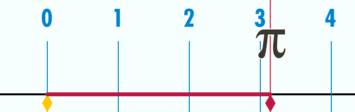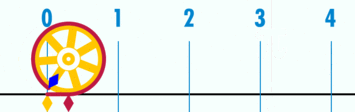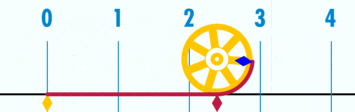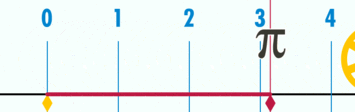
Площадь круга
Площадь круга - это количество плоскости, закрытой кругом. Мы можем представить круг как кусок пирога или тарелку, на которой расположены различные предметы. Площадь круга обозначается буквой "A".
Чтобы рассчитать площадь круга, нам понадобится еще одна формула. Если радиус круга равен "r", то площадь круга "A" равна произведению числа π (пи) на квадрат радиуса. Формула выглядит следующим образом:
\(A = π * r^2\)
Таким образом, чтобы найти площадь круга, нужно умножить квадрат радиуса на число π.
Связь между длиной окружности и площадью круга: Интересно отметить, что длина окружности и площадь круга связаны друг с другом. Если мы знаем длину окружности, мы можем использовать ее для расчета площади круга и наоборот.
Если нам дана длина окружности "C", то мы можем найти радиус круга "r" с помощью следующей формулы:
\(r = C / (2 * π)\)
Используя найденное значение радиуса, мы можем вычислить площадь круга "A" через длину окружности с помощью формулы:
\(A = π * r^2\)
Таким образом, мы можем использовать длину окружности для нахождения площади круга и наоборот.
Длина окружности и площадь круга - это два важных аспекта геометрии, связанные с окружностями и кругами. Зная радиус круга, мы можем легко рассчитать длину окружности и площадь круга с использованием соответствующих формул. Эти концепции имеют множество практических применений в различных областях, включая инженерию, архитектуру и науку.
Часто задаваемые вопросы
Как рассчитать длину окружности, если известен радиус круга?
Как рассчитать площадь круга, если известен его радиус?
Как связаны длина окружности и площадь круга?
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор по геометрии
Репетитор по геометрии -
 Репетитор для подготовки к ЕГЭ по химии
Репетитор для подготовки к ЕГЭ по химии -
 Репетитор для подготовки к ОГЭ по физике
Репетитор для подготовки к ОГЭ по физике -
 Подготовка к сочинению по русскому языку
Подготовка к сочинению по русскому языку -
 Репетитор по грамматике русского языка
Репетитор по грамматике русского языка -
 Репетитор по английскому ОГЭ
Репетитор по английскому ОГЭ -
 Подготовка к олимпиадам по английскому языку
Подготовка к олимпиадам по английскому языку -
 Репетитор по английскому для взрослых
Репетитор по английскому для взрослых -
 Репетитор по истории ОГЭ
Репетитор по истории ОГЭ -
 ВПР по физике
ВПР по физике


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

