Корень

Дарим в подарок бесплатный вводный урок!

Предметы

Специализации

В математике мы часто сталкиваемся с различными понятиями и символами, которые могут показаться нам загадочными и сложными. Одним из таких понятий является радикал. Но не волнуйтесь, сегодня мы погрузимся в увлекательный мир радикалов и узнаем, что они на самом деле означают.

Что такое радикал?

Радикал - это понятие, связанное с корнями в математике. Итак, что такое корень? Корень - это число, которое, возведенное в определенную степень, дает нам другое число. Например, квадратный корень из числа 9 равен 3, потому что 3 в квадрате равно 9. А теперь представьте, что радикал - это способ записи корня в математике.

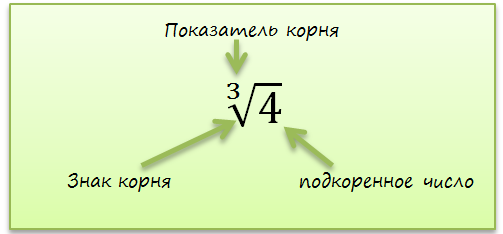
Радикал обычно записывается с помощью символа "√". Когда мы видим этот символ перед числом, это означает, что мы должны извлечь корень из этого числа. Например, √9 означает квадратный корень из числа 9, что равно 3. Точно так же, √16 означает квадратный корень из числа 16, что равно 4.

Вспомним рациональные числа: множество рациональных чисел \(Q\) (\(m/n\) , где \(m\) - целое число, а \(n\)– натуральное) включает в себя множество целых чисел, которое, в свою очередь, включает в себя множество натуральных чисел.

\( \sqrt{5}\) читается как корень из пяти, и если мы возьмем \(5^2\) ,то мы получим число \(5\). Корень - это обратная операция возведению в степень. Если \(n\) - положительное целое число, которое больше \(1\), а \(a-\)вещественное число, то:

\(^n \sqrt{a}=a^{\frac{1}{n}}\)

где \(n\) называется показателем, \(a\) - подкоренное выражение и сам символ читается корень из числа \(a\). Левую часть этого уравнения называют радикальной формой, а правую - экспоненциальной формой. Заметим, что показатель требуется для того чтобы убедиться, что мы правильно оцениваем корень.

Как работать с радикалами?

Когда мы работаем с радикалами, мы можем комбинировать их с другими математическими операциями: сложение, вычитание, умножение и деление. Например, мы можем складывать и вычитать радикалы с одинаковыми значениями под корнем, умножать и делить радикалы и числа и т.д.

Важно также понимать, что радикалы могут быть применены не только к положительным числам, но и к отрицательным и даже комплексным числам. Это позволяет нам работать с более широкими классами чисел и применять радикалы в различных математически

Пусть у нас есть некоторое число \( a ≥ 0\) и число \(n\) - натуральное число большее \(1\). Тогда существует единственное неотрицательное число x, такое, что выполняется равенство \(x^n=a\). В этом случае \(x\) называют арифметическим корнем \(n\)-й степени из неотрицательного числа a и обозначают: \(^n \sqrt{a}\)

Корень - это тот же радикал.

Извлечение корня - это арифметическая операция, обратная возведению в степень.

Степенью \(n\) числа \(a\) называют произведение \(n\) множителей, каждый из которых равен \(a\).

Если в радикальном выражении нет показателя, то показатель принимается равным \(2\), то есть пишут \( \sqrt{a} \), т.е. опускают показатель корня - и такое выражение называют квадратным корнем.

Часто задаваемые вопросы:

✅ Что такое радикал в математике?

↪ В математике радикал - это способ записи корня числа с помощью символа "√". Радикал указывает на извлечение корня из числа.

✅ Как найти значение радикала?

↪ Чтобы найти значение радикала, нужно извлечь корень из числа, указанного под знаком радикала. Например, √9 равно 3, так как это квадратный корень из числа 9.

✅ Как работать с радикалами в математических выражениях?

↪ При работе с радикалами в математических выражениях можно выполнять различные операции, такие как сложение, вычитание, умножение и деление. Например, можно складывать и вычитать радикалы с одинаковыми значениями под корнем, умножать и делить радикалы и числа, а также применять правила алгебры для упрощения выражений с радикалами.

Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Анна Александровна Ваструхина

Репетитор по математике

Стаж (лет)

Образование:

Краснодарский государственный университет культуры и искусств

Проведенных занятий:

148

Форма обучения:

Дистанционно (Скайп)

Надежда Геннадьевна Зубкова

Репетитор по математике

Стаж (лет)

Образование:

Астраханский педагогический университет

Проведенных занятий:

1135

Форма обучения:

Дистанционно (Скайп)

Виолетта Грантовна Саркисян

Репетитор по математике

Стаж (лет)

Образование:

Тбилисский Государственный Педагогический Университет

Проведенных занятий:

1946

Форма обучения:

Дистанционно (Скайп)