Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Функция обратной пропорциональности
Характеристики функции k/x
График \(y =\frac{k}{x}\) приближается к оси \(x\) по мере увеличения значения \(x \), но никогда не встречается с осью \(X\). Это называется горизонтальной асимптотой графика.
Каждая часть графика также становится ближе к оси \(y\), поскольку \(x\) приближается к \(0\), но никогда не встречается с осью \(y\), поэтому нет значения для \(y\), когда \(x = 0\). Это называется вертикальной асимптотой графика. Этот тип функции называется гиперболой, где \(k-\) действительное число и \(x ≠ 0\).
Пример 1. Постройте график функции \(y =\frac{5}{x}\).
Решение.
![]()
![]()
- Выберем произвольные точки \(x \) и посчитаем соответсвующие им значения \(y\) :
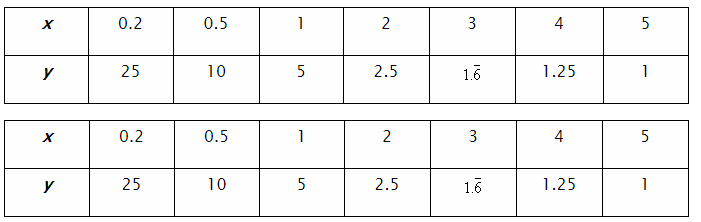
- Построим точки из таблицы и плавно соединим их:
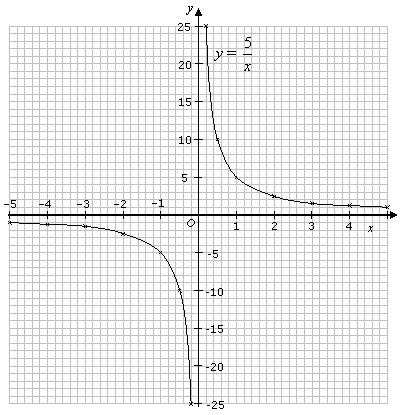
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор для подготовки к ЕГЭ по химии
Репетитор для подготовки к ЕГЭ по химии -
 Репетитор для подготовки к ОГЭ по химии
Репетитор для подготовки к ОГЭ по химии -
 Подготовка к олимпиадам по химии
Подготовка к олимпиадам по химии -
 Репетитор для подготовки к ОГЭ по физике
Репетитор для подготовки к ОГЭ по физике -
 Репетитор для подготовки к ЕГЭ по английскому
Репетитор для подготовки к ЕГЭ по английскому -
 Репетитор по английскому с нуля
Репетитор по английскому с нуля -
 Репетитор по разговорному английскому
Репетитор по разговорному английскому -
 Репетитор ЕГЭ по обществознанию
Репетитор ЕГЭ по обществознанию -
 Подготовка к ЕГЭ по биологии онлайн
Подготовка к ЕГЭ по биологии онлайн -
 Онлайн репетитор ОГЭ по биологии
Онлайн репетитор ОГЭ по биологии


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

