Задачи на движение по прямой (вариант 1)

 
Задача № 1
 
Два велосипедиста одновременно отправились в 88–километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
 
Решение
 
Пусть "х" км/ч – скорость велосипедиста, пришедшего к финишу вторым, тогда скорость первого велосипедиста равна:
 
х + 3 км/ч.
 
Первый велосипедист прибыл к финишу на 3 часа раньше второго, отсюда можем записать уравнение, имеем:
 
 
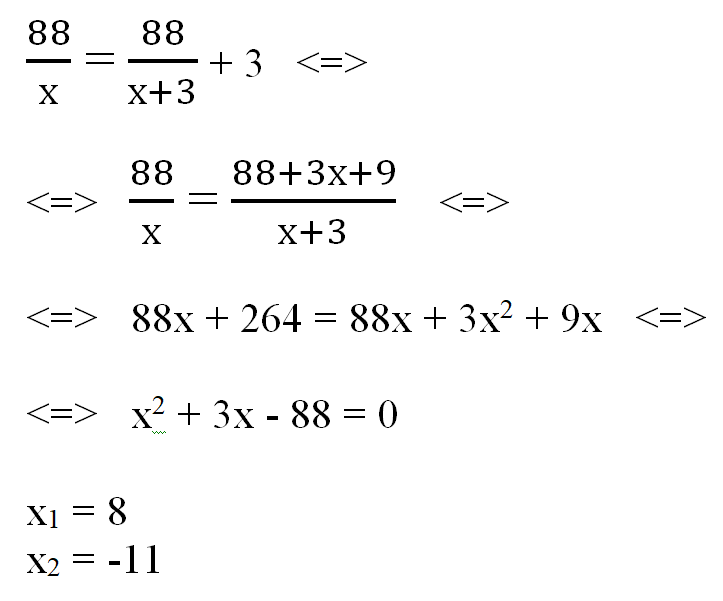
Так как по условию задачи х > 0, то корень х2 = -11 не подходит.
 
Таким образом, скорость велосипедиста, пришедшего к финишу вторым, равна 8 км/ч.
 
Ответ: 8.
 
 
Задача № 2
 
Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
 
Решение
 
Пусть "у" часов – время движения автомобилей до встречи. Первый автомобиль пройдет расстояние "65у" км, а второй – "75у" км.
Тогда имеем:
 
65у + 75у = 560  <=>
 
<=>   140у = 560    <=>
 
<=>   у = 4
 
Таким образом, автомобили встретятся через 4 часа.
 
Ответ: 4.
 
 
Задача № 3
 
Из городов А и В, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города В. Найдите скорость автомобиля, выехавшего из города А. Ответ дайте в км/ч.
 
Решение
 
Из условия задачи видно, что автомобиль, выехавший из города А, преодолел расстояние:
 
330 – 180 = 150 км
 
Он преодолел это расстояние за 3 часа.
 
Пусть "V" км/ч – скорость данного автомобиля.
 
Таким образом, из формулы:
 
\(V={s\over t}\)
 
Подставив числовые значения, получим:
 
\(V={150\over 3}=50 \) км/ч
 
Ответ: 50.
 
 
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Людмила Владимировна Коченова
Репетитор по математике
Стаж (лет)
19
Образование:
Южно-Российский государственный политехнический университет им. М.И. Платова
Проведенных занятий:
1419
Форма обучения:
Дистанционно (Скайп)
Фёдор Владимирович Каузов
Репетитор по математике
Стаж (лет)
3
Образование:
Государственное образовательное учреждение высшего профессионального образования Ивановский государственный университет
Проведенных занятий:
16
Форма обучения:
Дистанционно (Скайп)
Галина Федоровна Захарина
Репетитор по математике
Стаж (лет)
6
Образование:
Гомельский государственный университет имени Ф. Скорины
Проведенных занятий:
2071
Форма обучения:
Дистанционно (Скайп)
Предметы
Специализации
Похожие статьи