Как решить квадратное уравнение

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Квадратное уравнение – что это?
Как выглядит квадратное уравнение?
Как же решать квадратное уравнение?
Как найти дискриминант квадратного уравнения
Как решать квадратные уравнения через дискриминант
Примеры решения квадратных уравнений с помощью дискриминанта
Часто задаваемые вопросы:

Обновлено: 16 сен 2024

Как решить квадратное уравнение

Квадратное уравнение – что это?

Квадратное уравнение – это уравнение, которое имеет вид:

\(ax^2+bx+c=0\)

Что такое a, b и с? Это коэффициенты. У каждого есть свои названия:

а – старший коэффициент;

b – средний коэффициент;

с – свободный член;

a, b, c – абсолютно любые числа. Но здесь важно: а ≠ 0.

Почему именно так? Давай поразмышляем: если предположить, что а все же будет равно 0, то наше уравнение уже не будет квадратным и превратится в линейное:

\(bx+c=0\)

А такие уравнения ты уже решать умеешь, поэтому мы вернемся обратно к квадратным уравнениям.

Как выглядит квадратное уравнение?

К слову, квадратное уравнение может выглядеть необязательно как стандартное: \(ax^2+bx+c=0\)

Оно может иметь и другой вид, например:

\(ac^2+bx=c\)

(здесь свободный член с находится по другую сторону знака равно) или \(ax^2=c\) (тут средний коэффициент b = 0, а с находится по другую сторону знака равно). Также коэффициенты могут быть отрицательными и т.д.

Однако следует помнить, что абсолютно любое квадратное уравнение можно привести к стандартному виду:

\(ax^2+bx+c=0\)

Как же решать квадратное уравнение?

Существует всего три результата решения квадратного уравнения:

Уравнение не имеет решения.
Уравнение имеет только один корень.
Уравнение имеет два корня.

Как определить, под какой из этих случаев подпадет наше квадратное уравнение? Для этого нам понадобится дискриминант: он нам поможет в решении квадратного уравнения. Дискриминантом (образован от латинского discrimino – «разбираю») мы обозначим следующее выражение:

\(D=b^2-4ac\),

где D – дискриминант, а a, b, c – коэффициенты квадратного уравнения.

Чем конкретно нам может помочь дискриминант?

Если D < 0 – то квадратное уравнение не имеет решений;
Если D = 0 – то уравнение будет иметь только один корень;
Если D > 0 – то уравнение имеет два решения.

То есть благодаря дискриминанту мы будем знать о результате и количестве решений квадратного уравнения.

Итак, мы посчитали, чему равен наш дискриминант, потом определили количество решений уравнения, что дальше? А дальше определяем корни квадратного уравнения по формулам.

В первом случае, когда D < 0, считать ничего не нужно, т.к. уравнение не имеет решений. Это значит, что корней квадратного уравнения на множестве действительных чисел нет.
Во втором варианте, когда D = 0, решение будет одно и единственный корень квадратного уравнения будет равен: \(x=\frac{-b}{2a}\)
Третий случай, при D > 0, наиболее сложный из всех трех возможных: в ответе должно получиться два корня квадратного уравнения.

\(x_1=\frac{-b+\sqrt D}{2a}\)– первый корень квадратного уравнения;

\(x_1=\frac{-b-\sqrt D}{2a}\)– второй корень квадратного уравнения.

Как найти дискриминант квадратного уравнения

Дискриминант квадратного уравнения — это выражение, равное b2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D < 0, то корней нет.
Если D = 0, то есть один корень, равный −b/2a.
Если D > 0, то у уравнения две корня, равные.

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x2 - 4x + 2 = 0.

Как решаем:

Определим коэффициенты: a = 3, b = -4, c = 2.

Найдем дискриминант: D = b2 - 4ac = (-4)2 - 4 * 3 * 2 = 16 - 24 = -8.
Ответ: D < 0, корней нет.

Пример 2. Решить уравнение: x2 - 6x + 9 = 0.

Как решаем:

Определим коэффициенты: a = 1, b = -6, c = 9.

Найдем дискриминант: D = b2 - 4ac = (-6)2 - 4 * 1 * 9 = 36 - 36 = 0.

D = 0, значит уравнение имеет один корень:

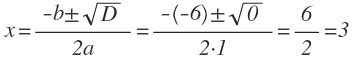
Ответ: корень уравнения 3.

Решение квадратных уравнений на самом деле не настолько сложное, как кажется на первый взгляд. Всего-то нужно запомнить несколько формул и алгоритм действий. Главное - не бояться вида квадратных уравнений, мы уверены: все у тебя получится! Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

Часто задаваемые вопросы:

✅ Что такое квадратное уравнение?

↪ Квадратное уравнение - это уравнение вида \(ax^2 + bx + c = 0\), где a, b, и c - коэффициенты, x - переменная.

✅ Как решить квадратное уравнение?

↪ Квадратное уравнение можно решить, используя формулу Квадратного корня: \(x = (-b ± √(b^2 - 4ac)) / 2a\). Необходимо вычислить значение выражения под корнем и подставить его в формулу.

✅ Каковы особенности решения квадратного уравнения?

↪ Квадратное уравнение может иметь два, один или ноль корней. Количество корней зависит от дискриминанта \(D = b^2 - 4ac\). Если D > 0, то уравнение имеет два корня, если D = 0, то уравнение имеет один корень, если D < 0, то уравнение не имеет корней в области действительных чисел.

Следующая статья