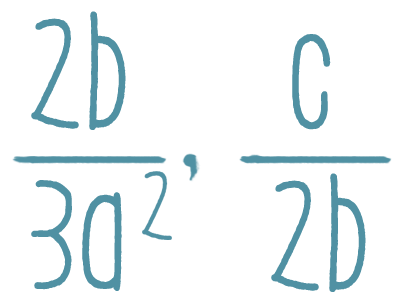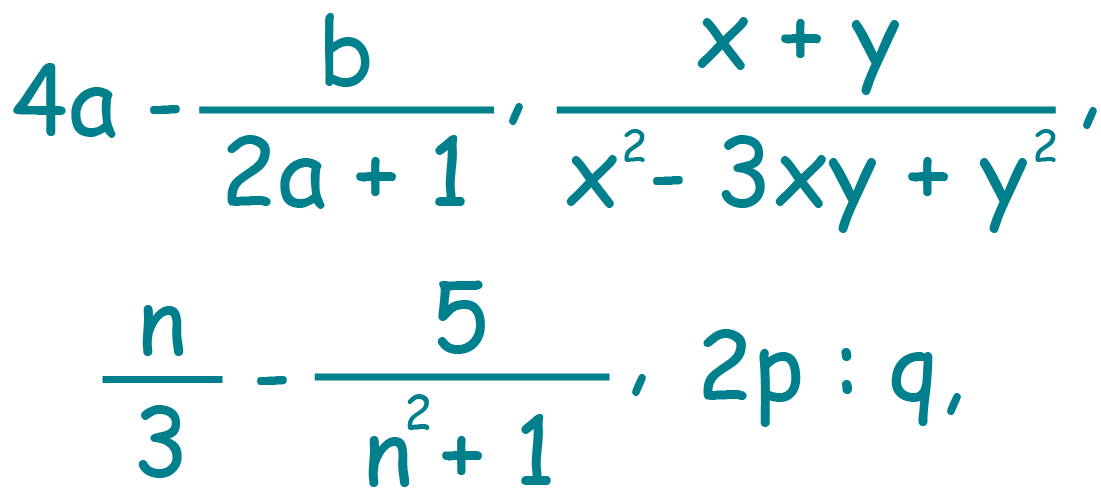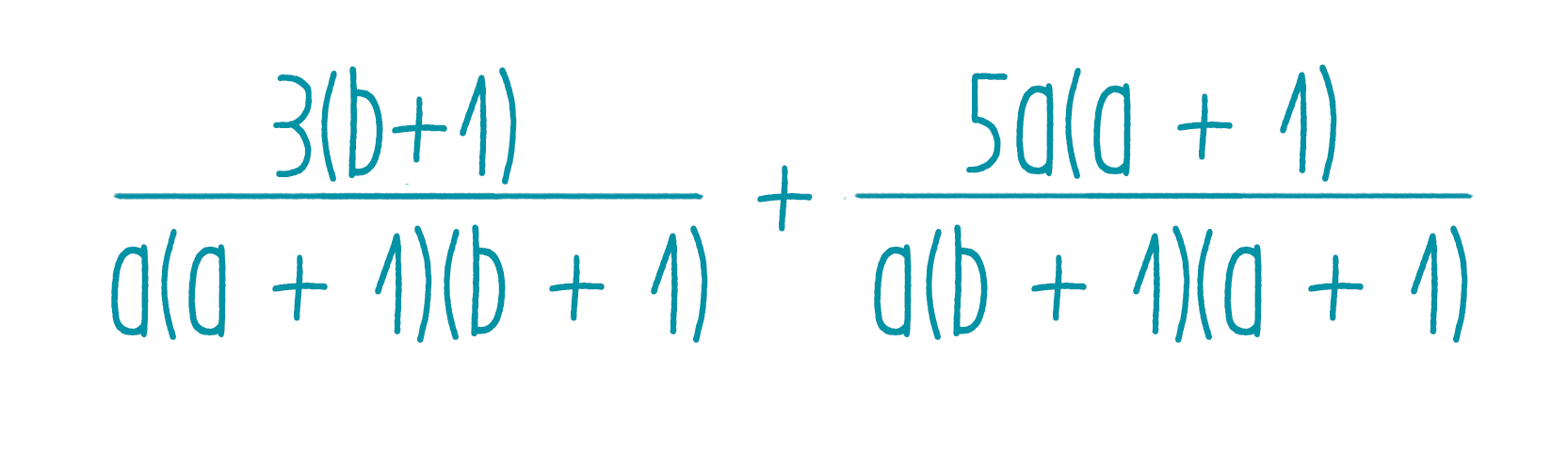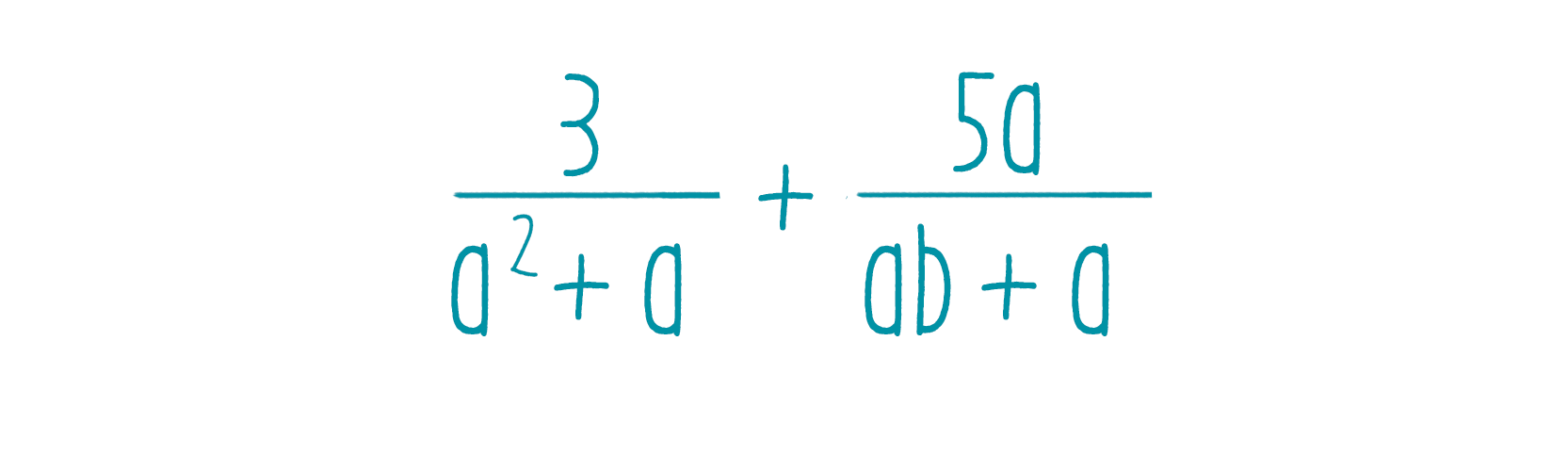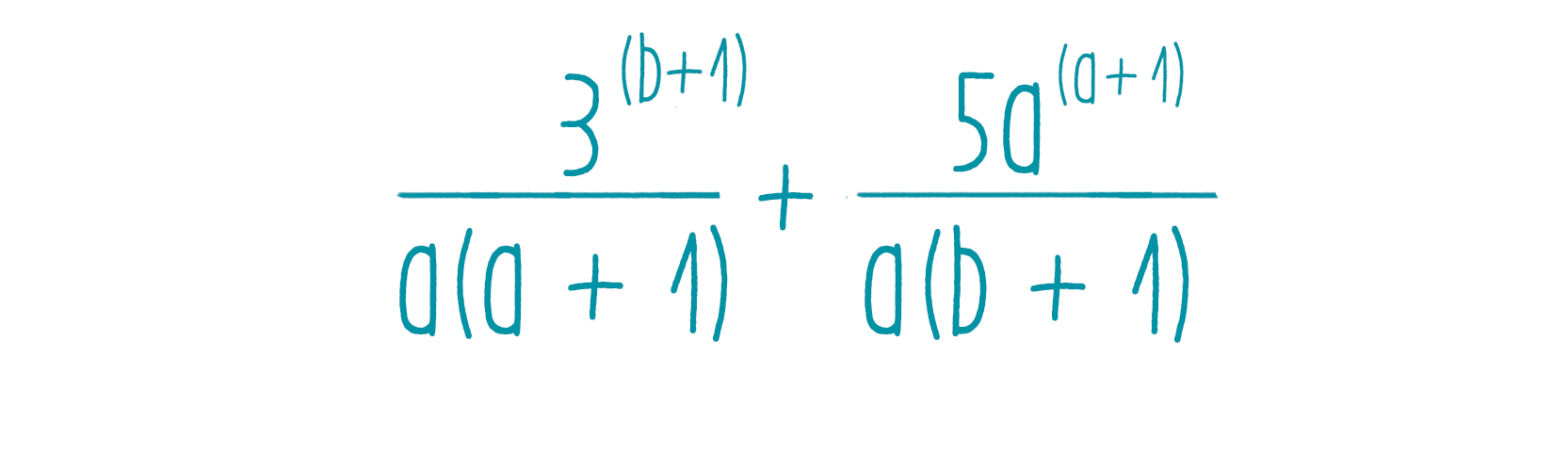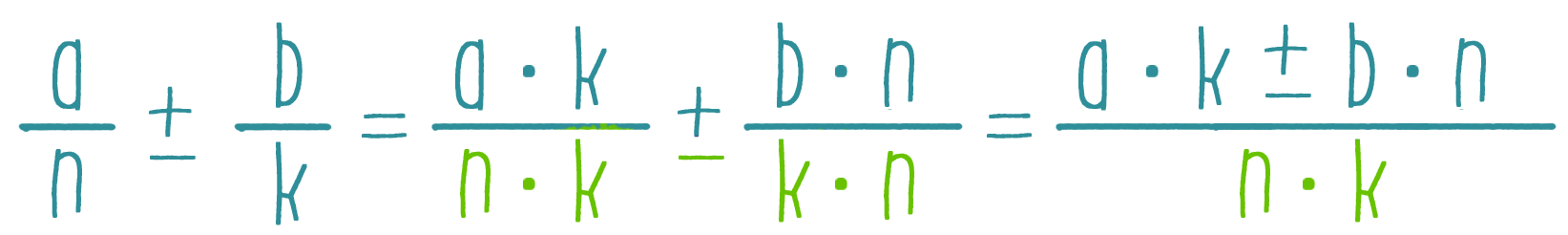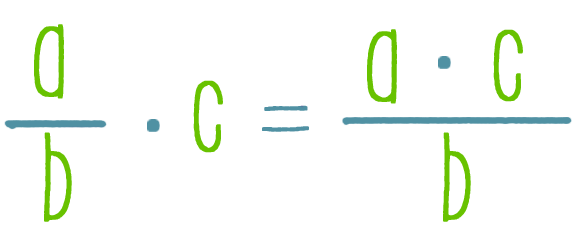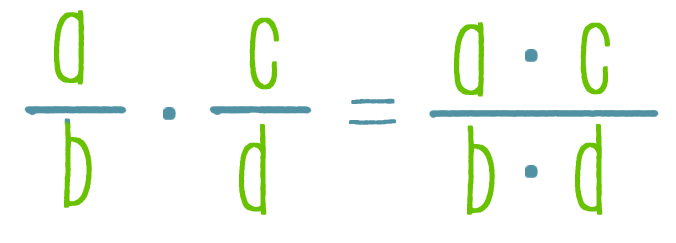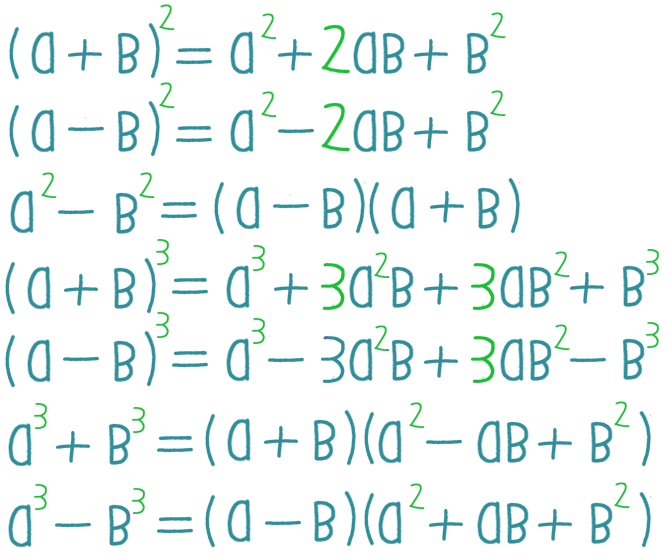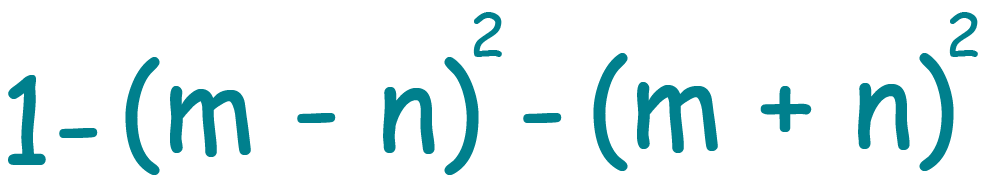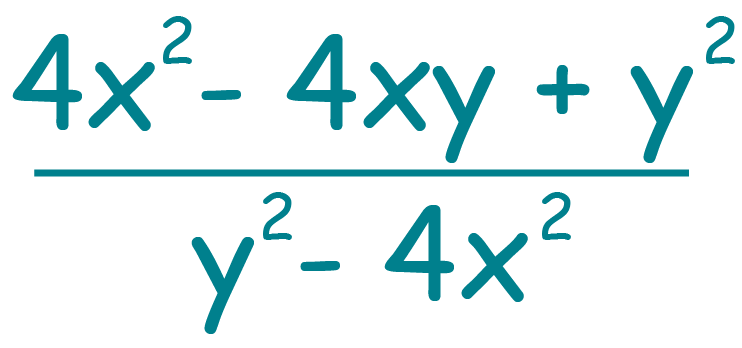Тождественное равенство рациональных выражений - онлайн урок




Тождественное равенство рациональных выражений

Отзывы:
Преподаватель:
Амина
Амине очень понравился урок. Интересно, увлекательно.
Преподаватель:
Лана
Прекрасный репетитор, позволяет с удовольствием заниматься уроком! Спасибо, было круто!
Преподаватель:
Дима
Интересный урок. Сыну очень понравилось. Будем ещё заниматься


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход