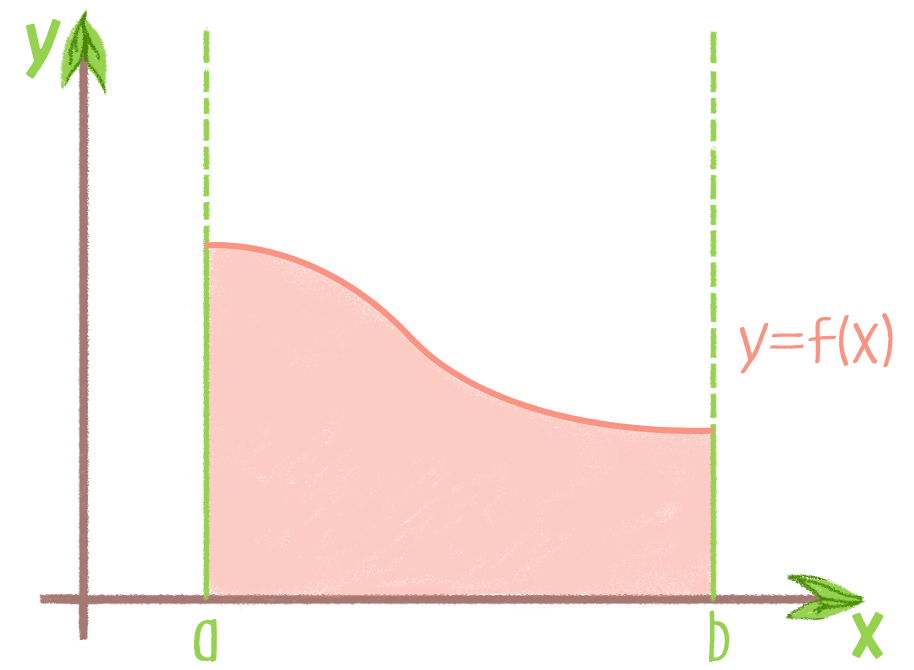
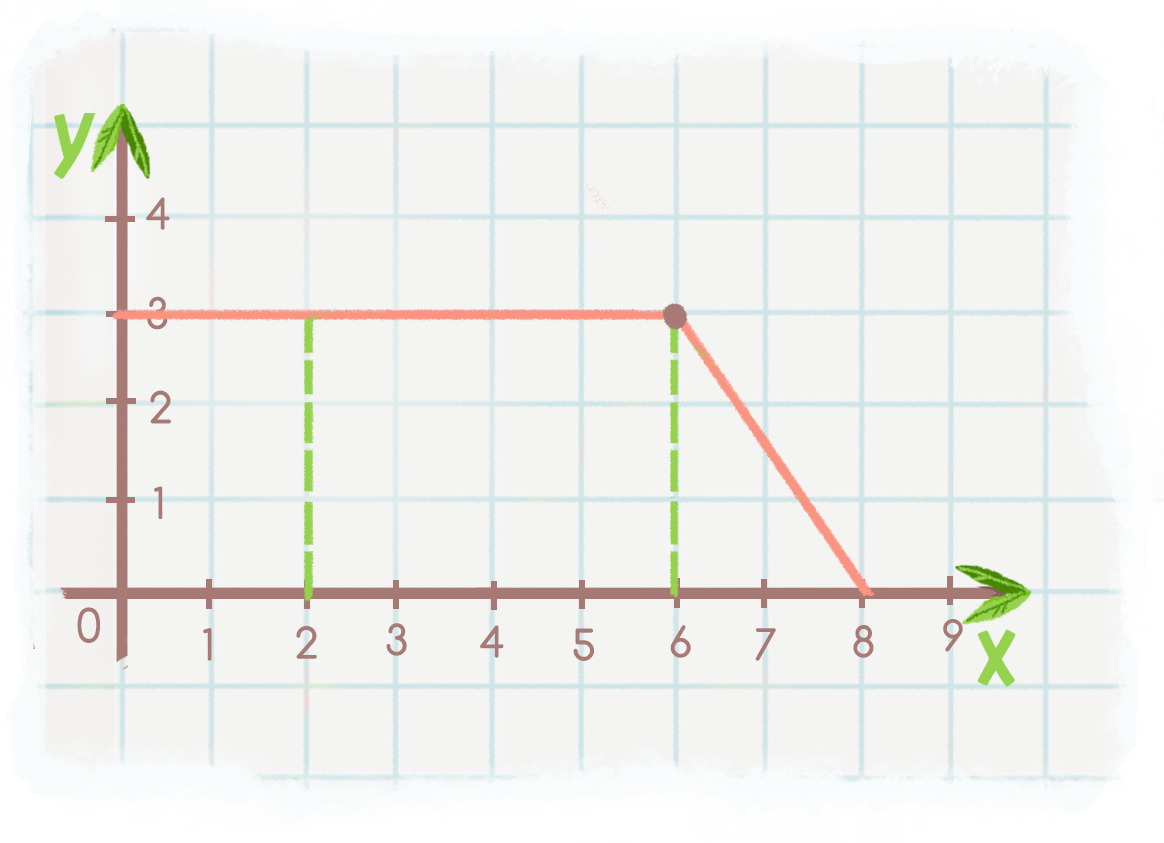
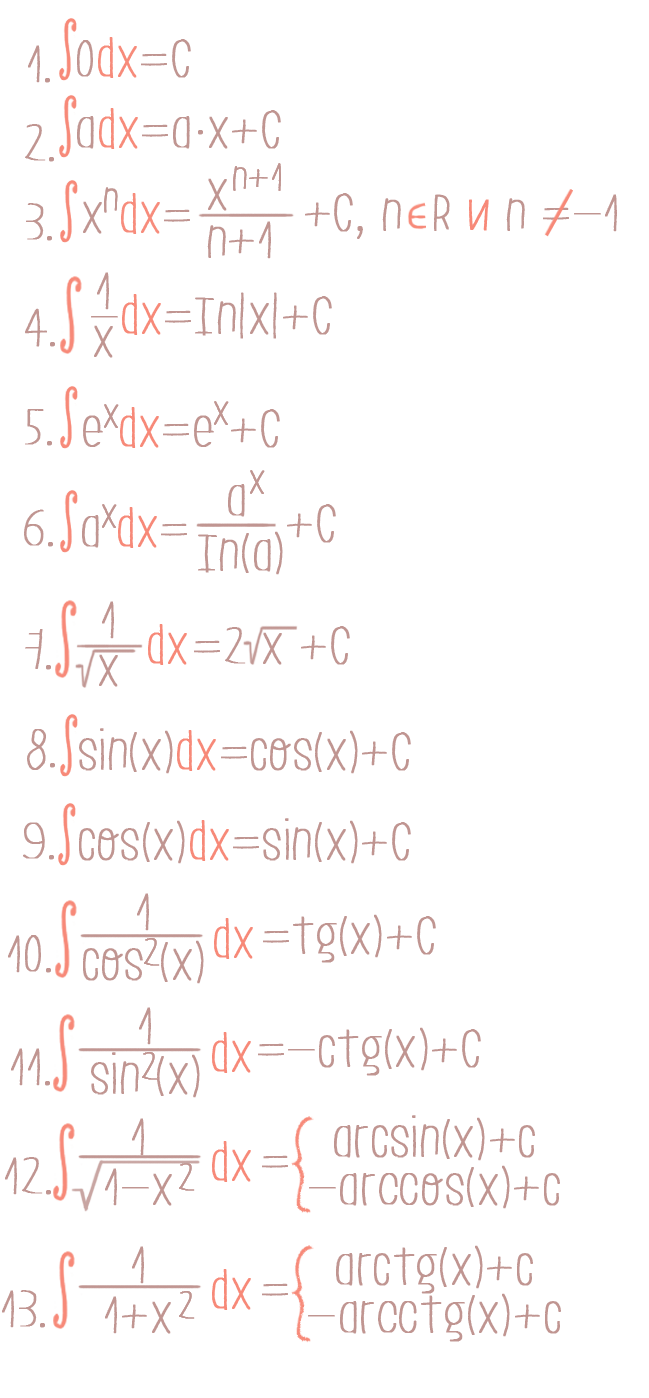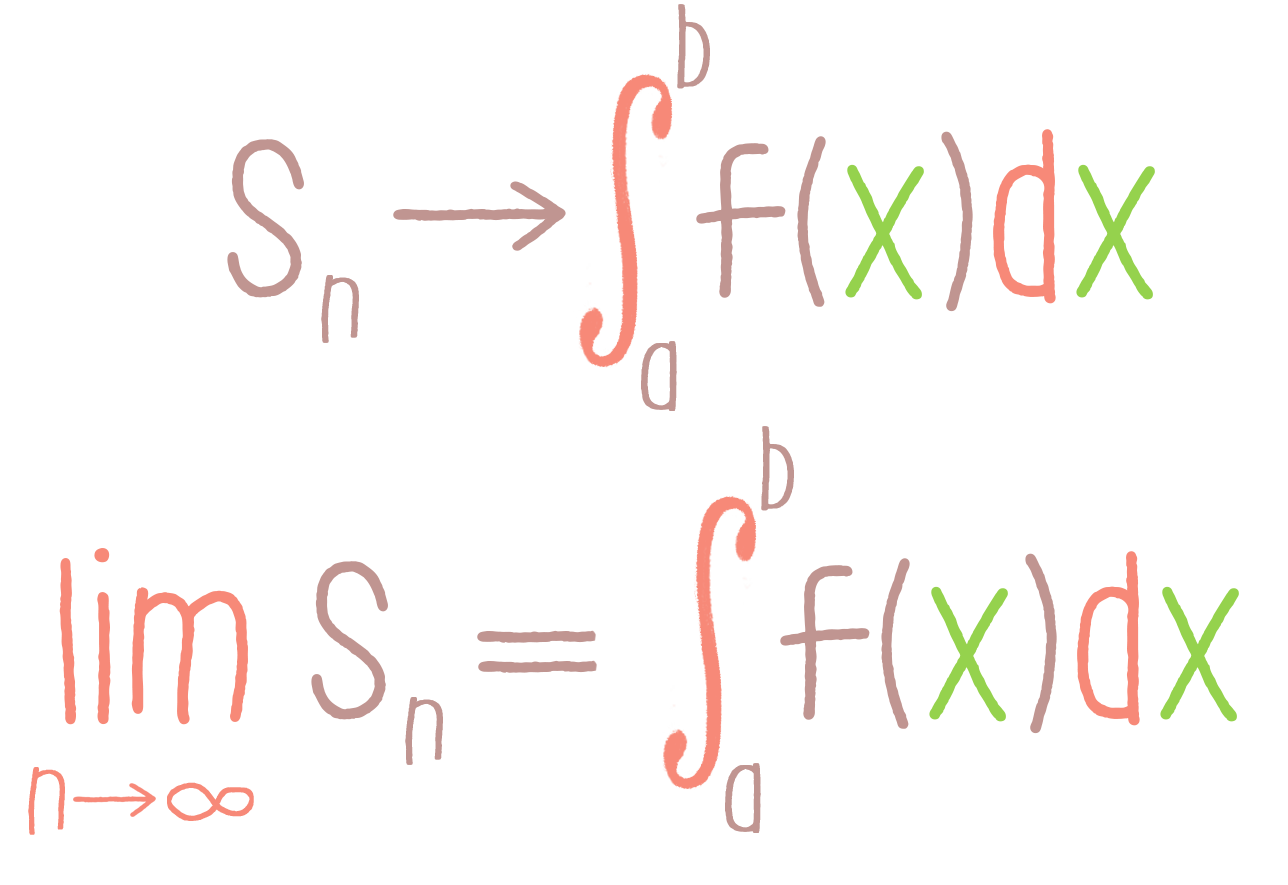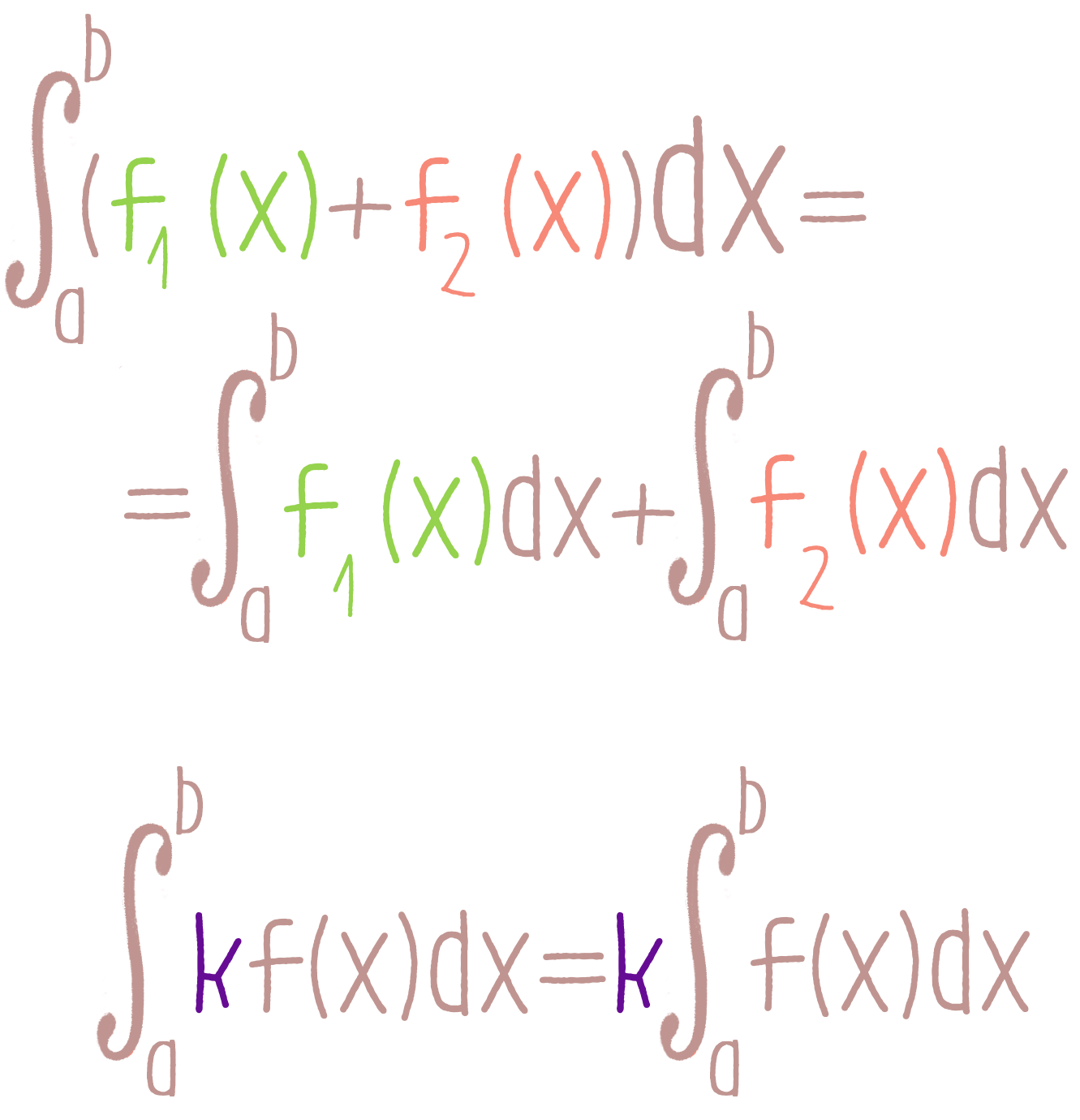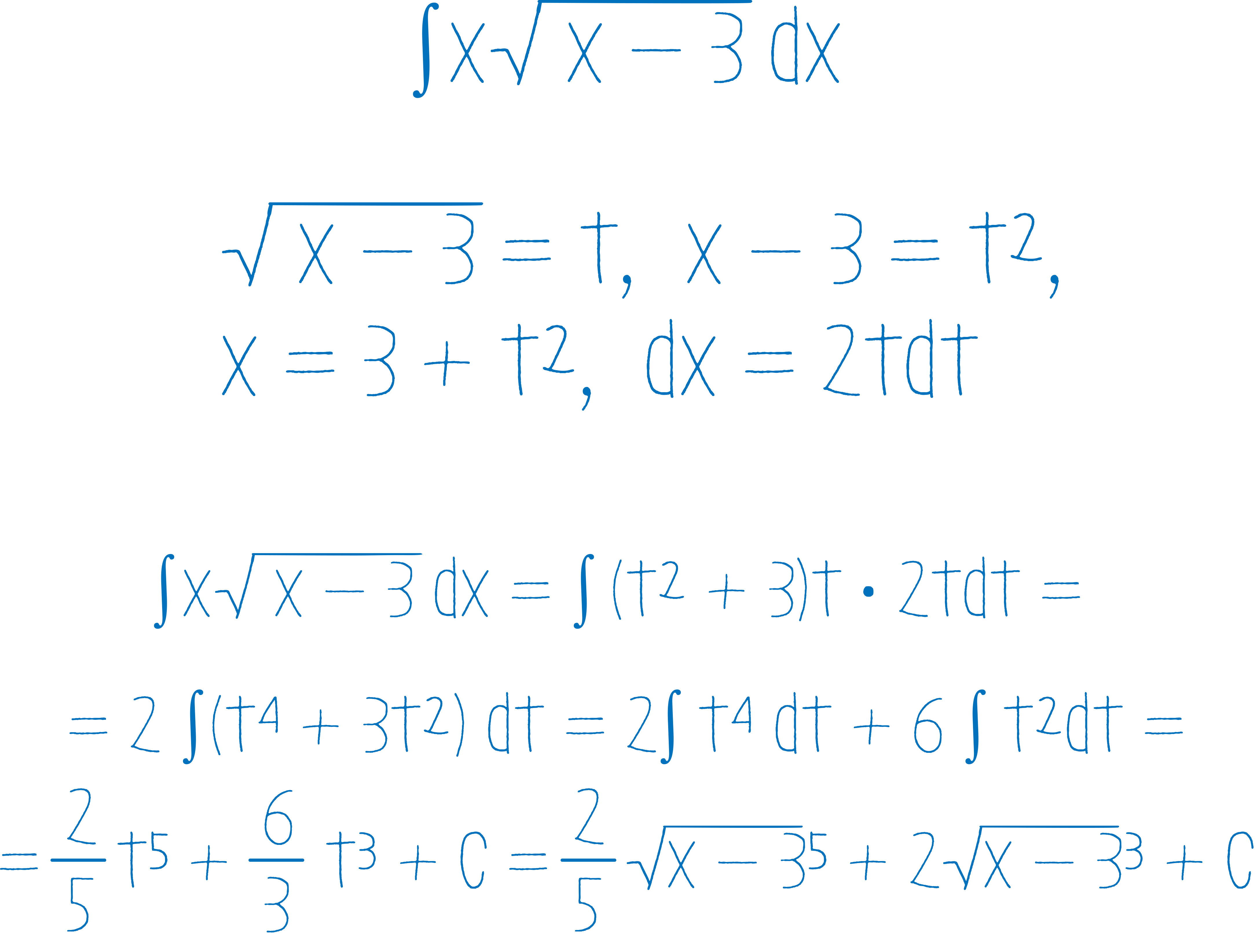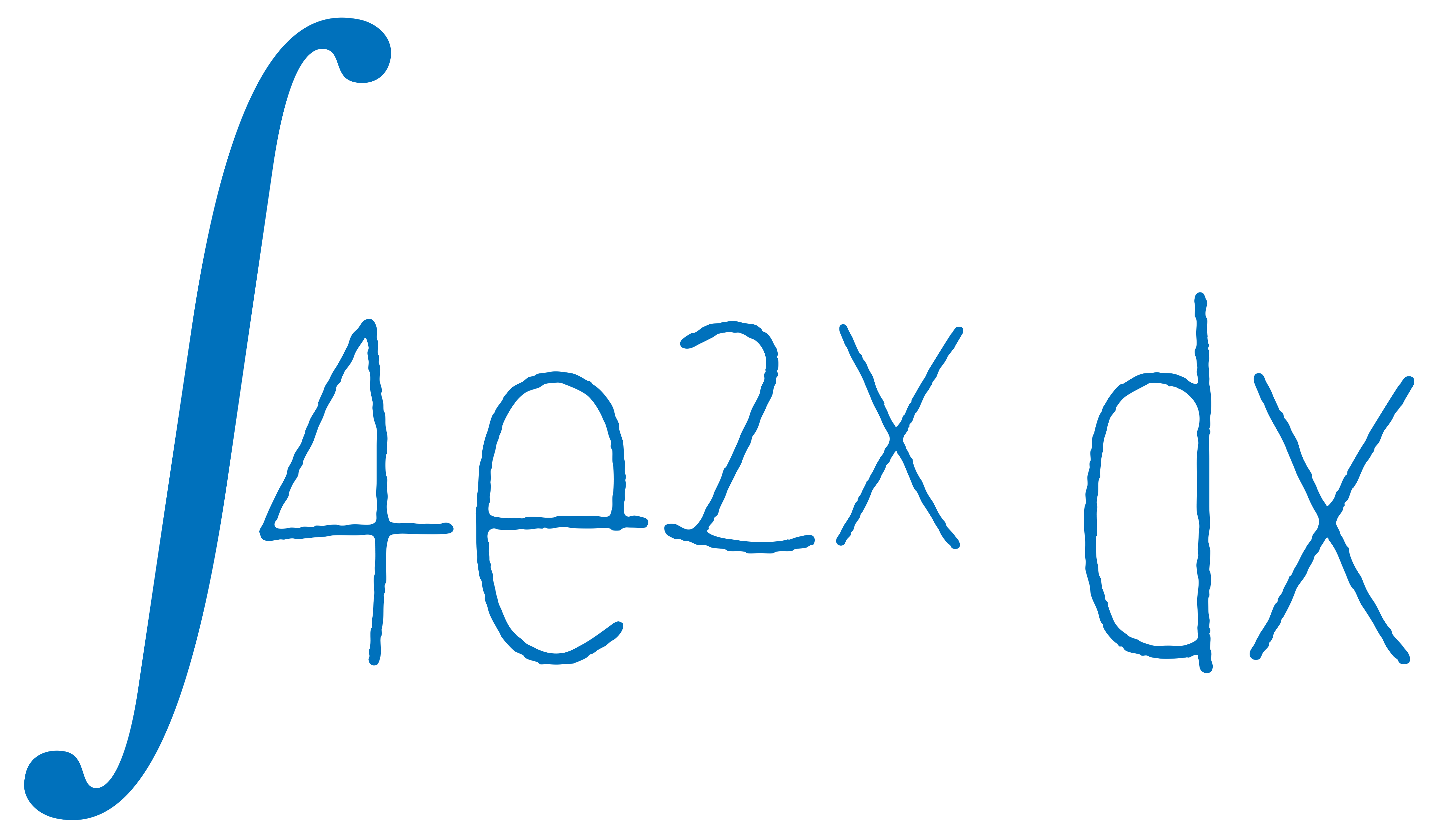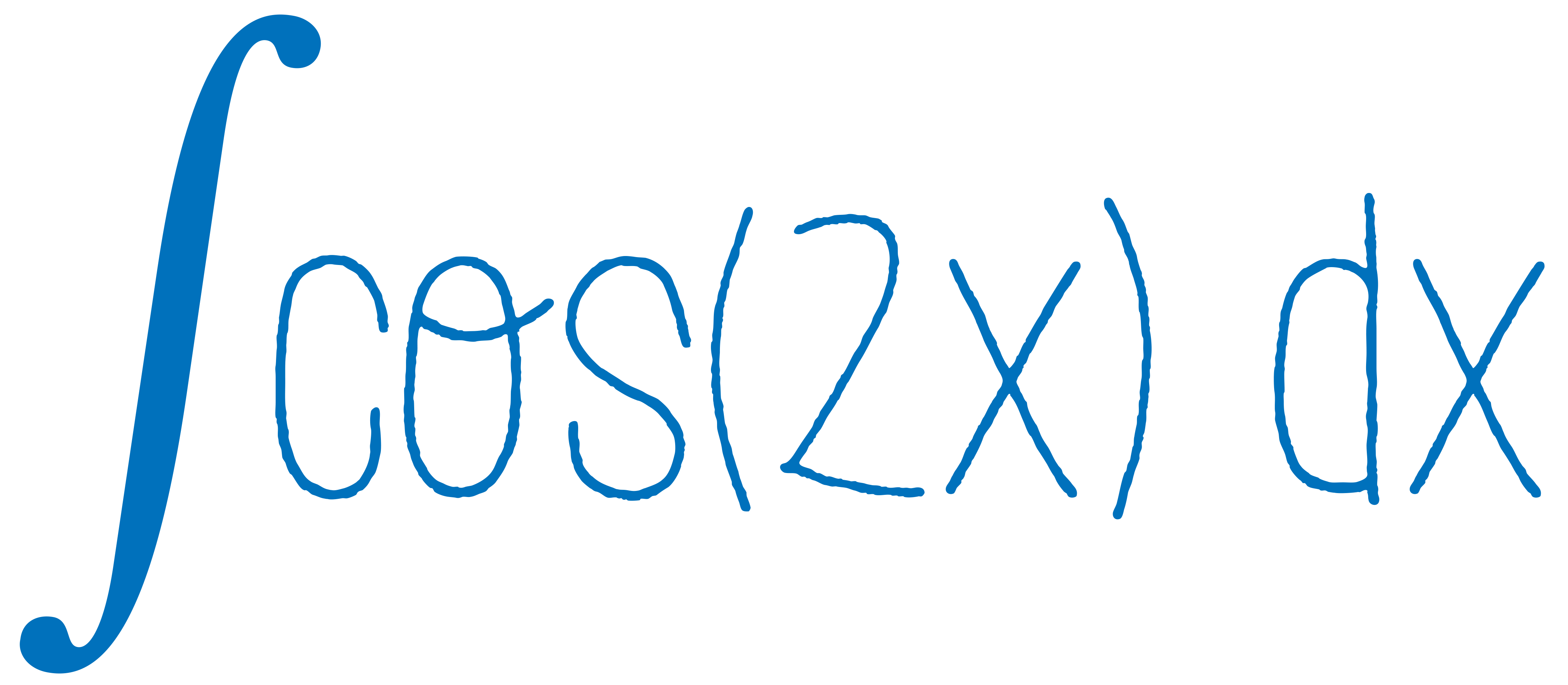Уравнения с разделяющимися переменными - онлайн урок




Уравнения с разделяющимися переменными

Похожие уроки


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход