Radian and degree measures of angles. - онлайн урок




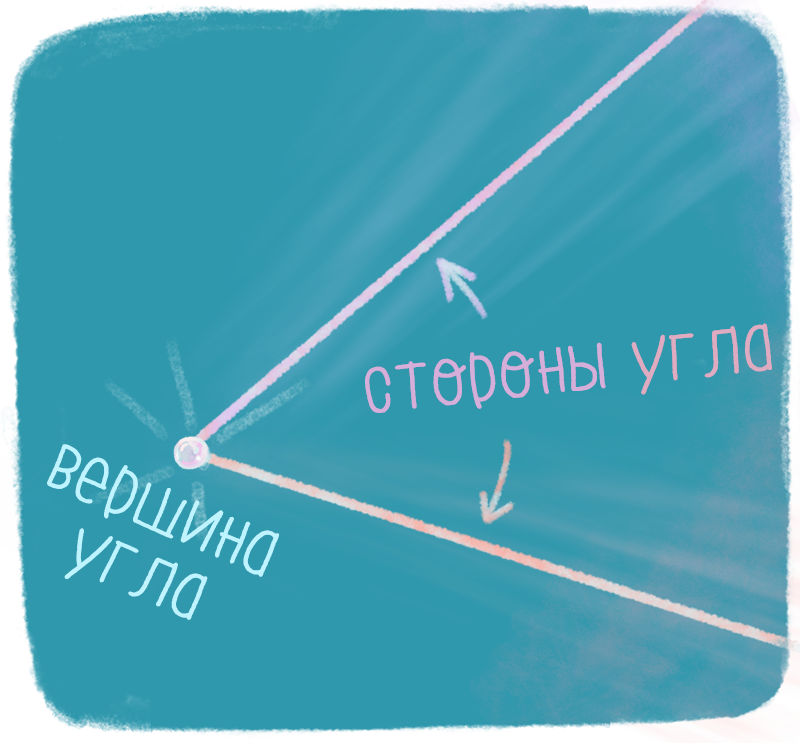
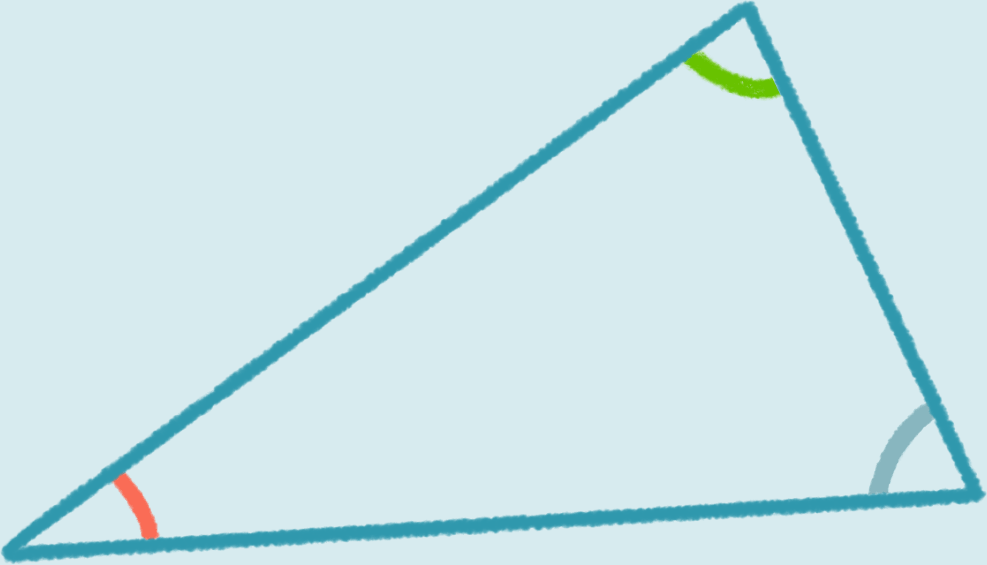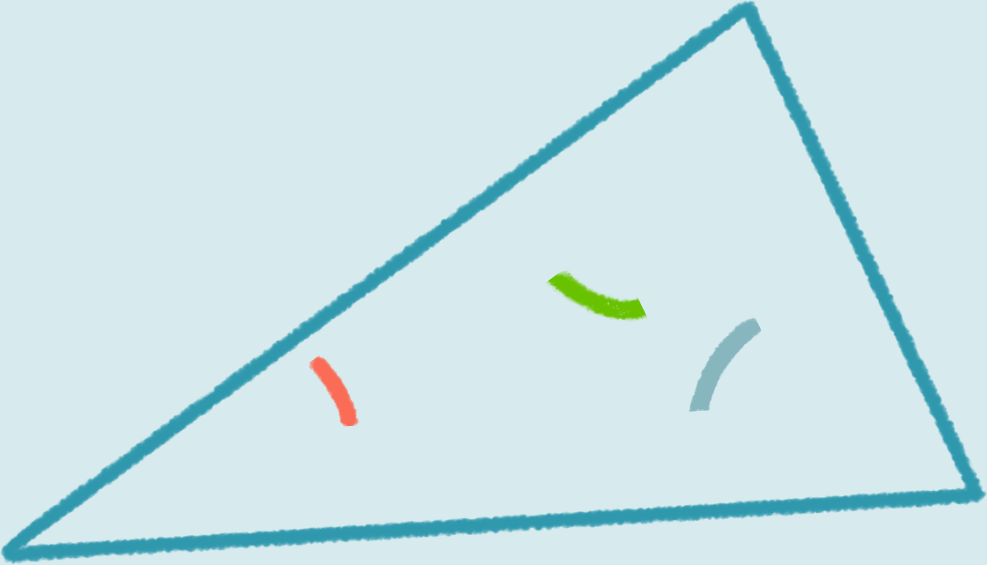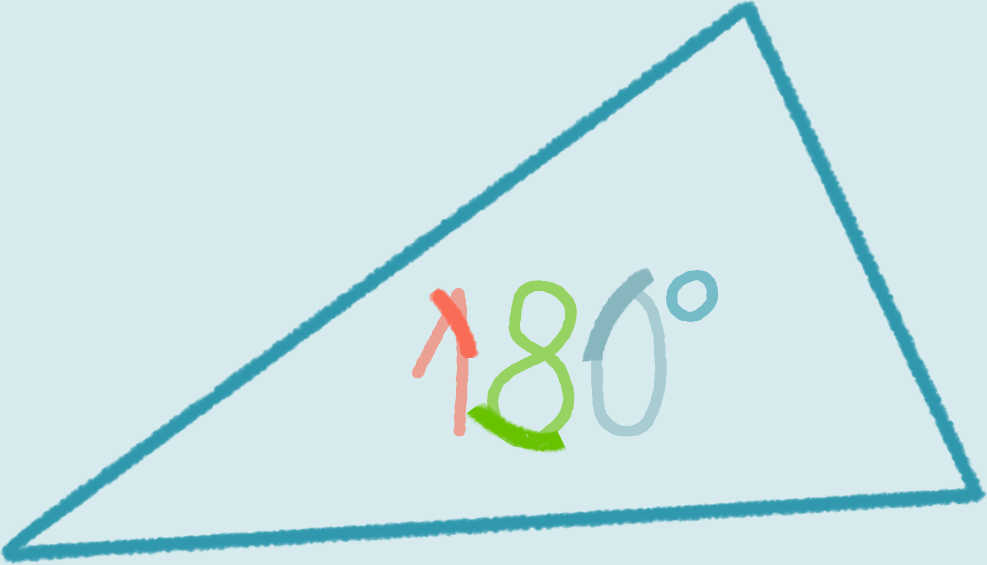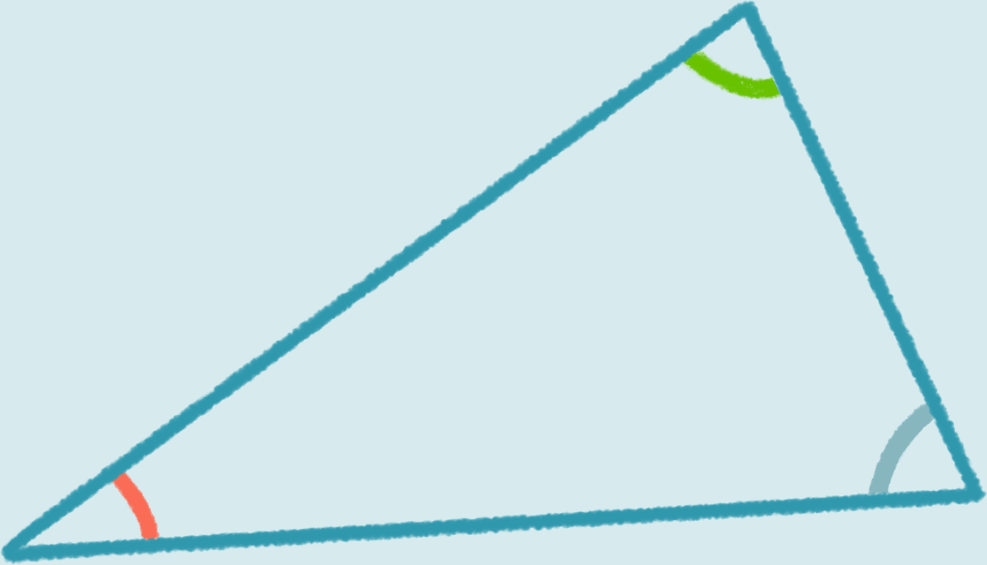
Radian and degree measures of angles.

Похожие уроки


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход