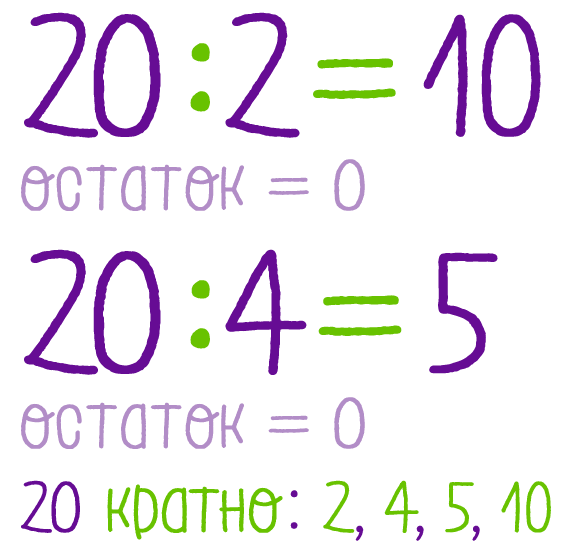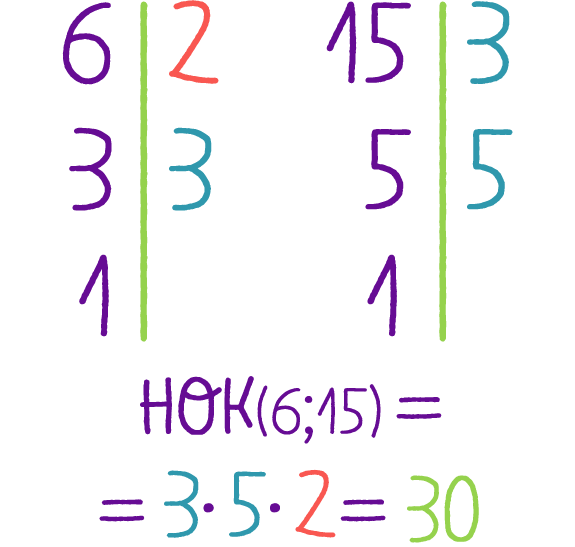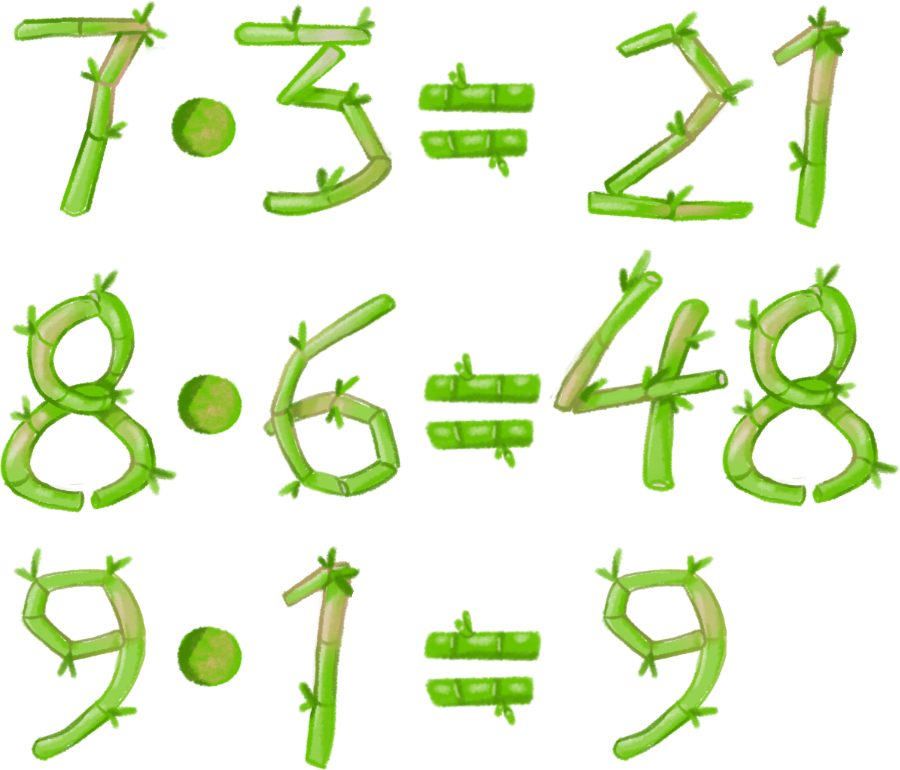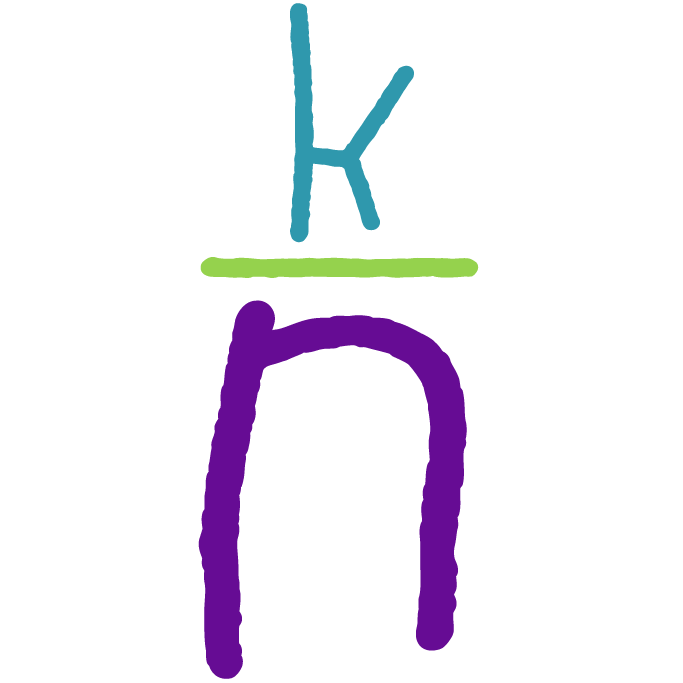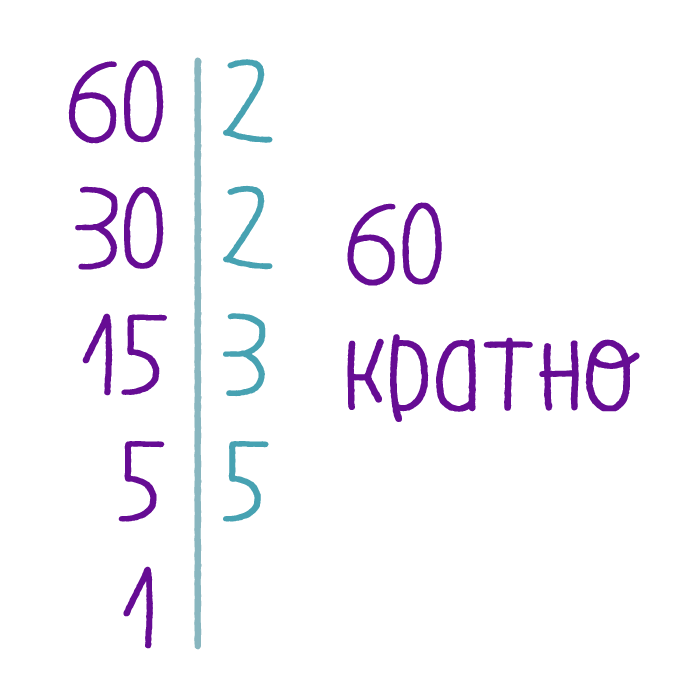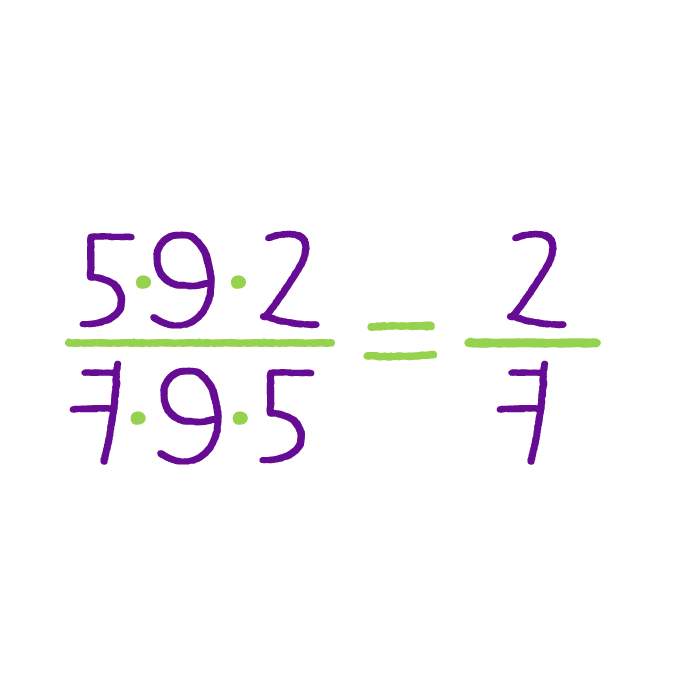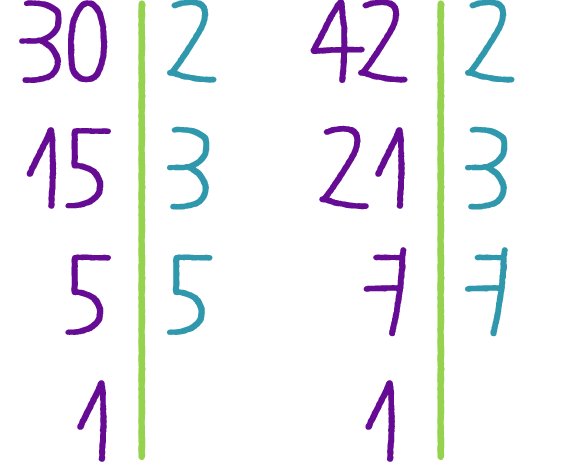Приведение к общему знаменателю. - онлайн урок




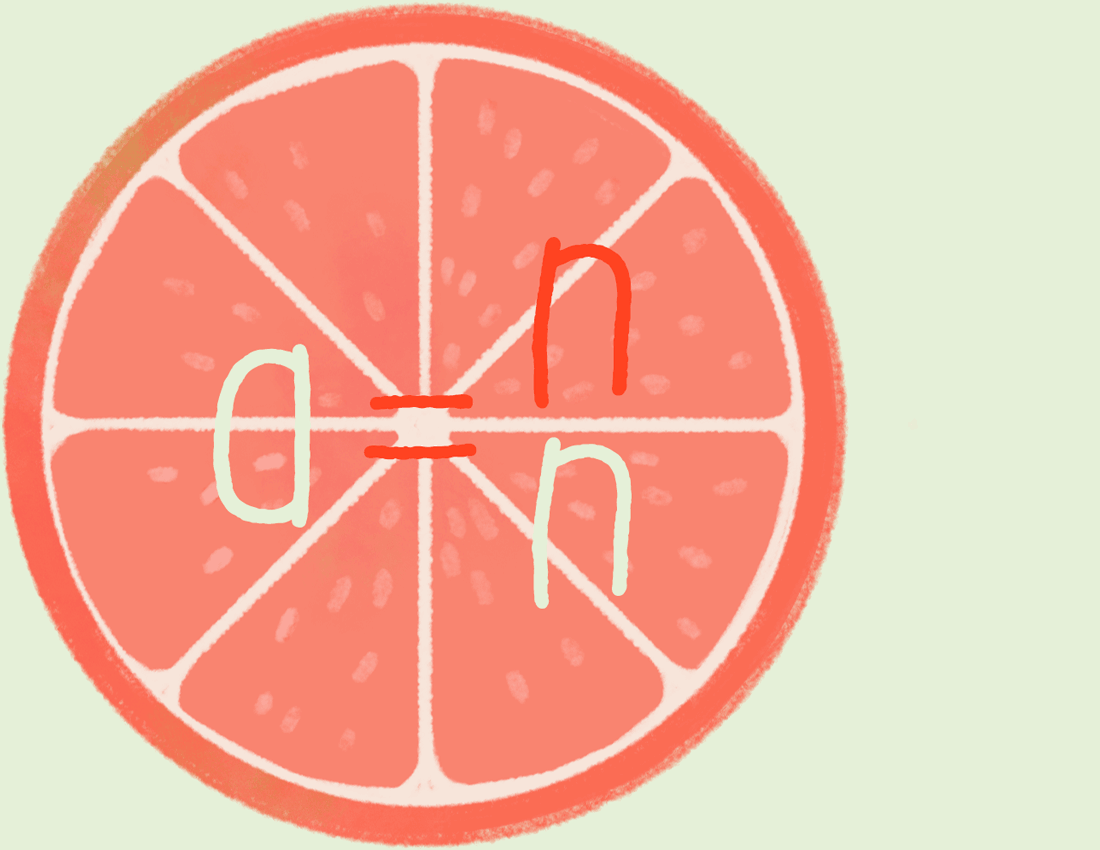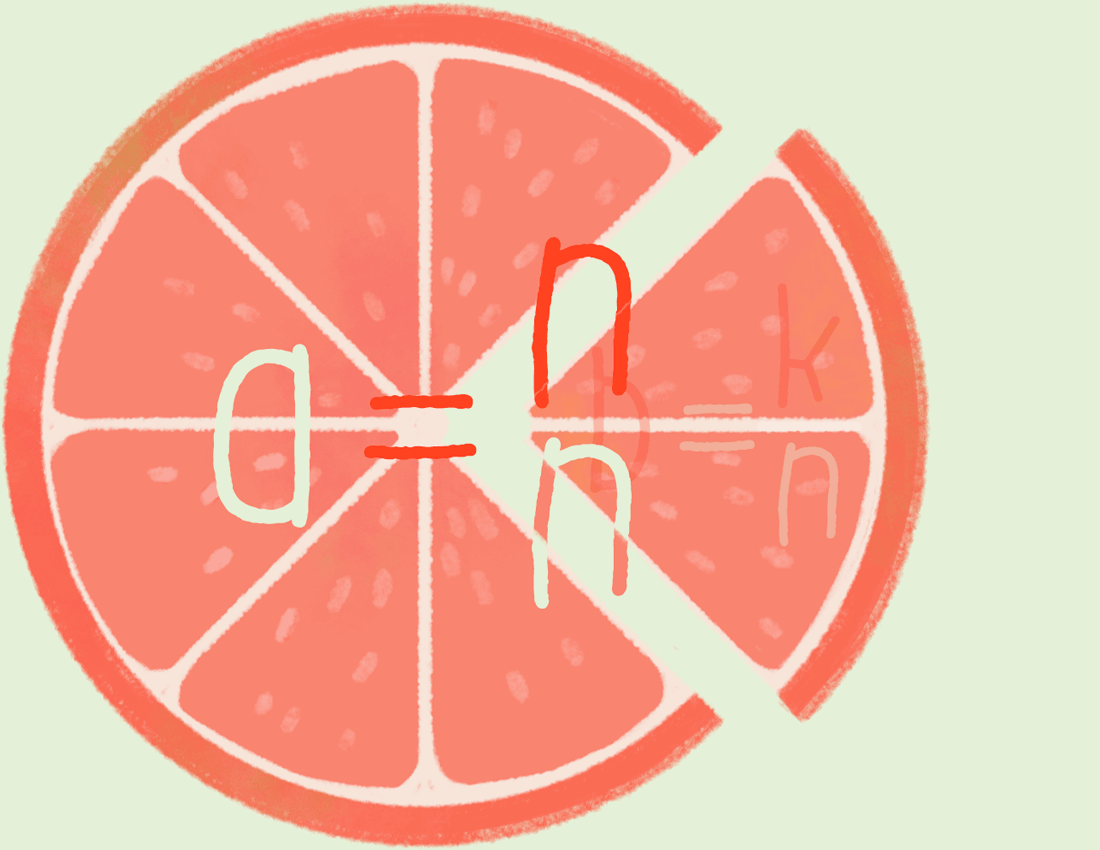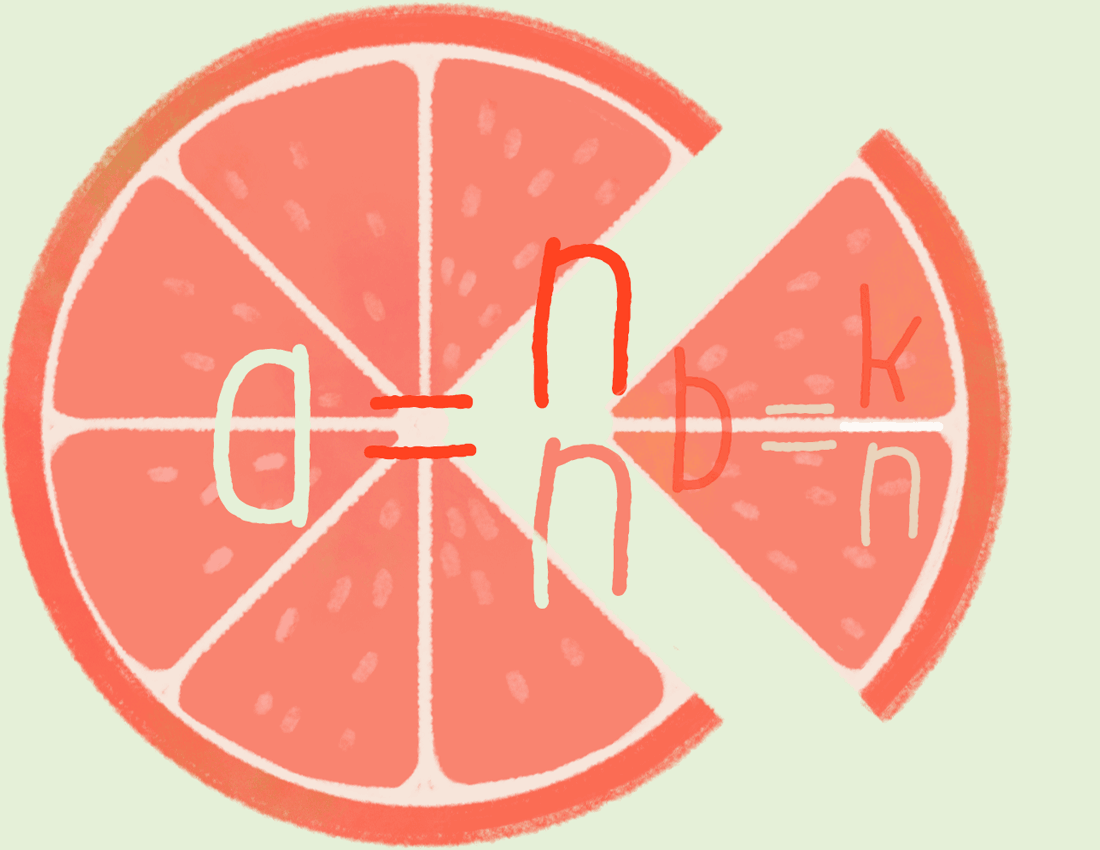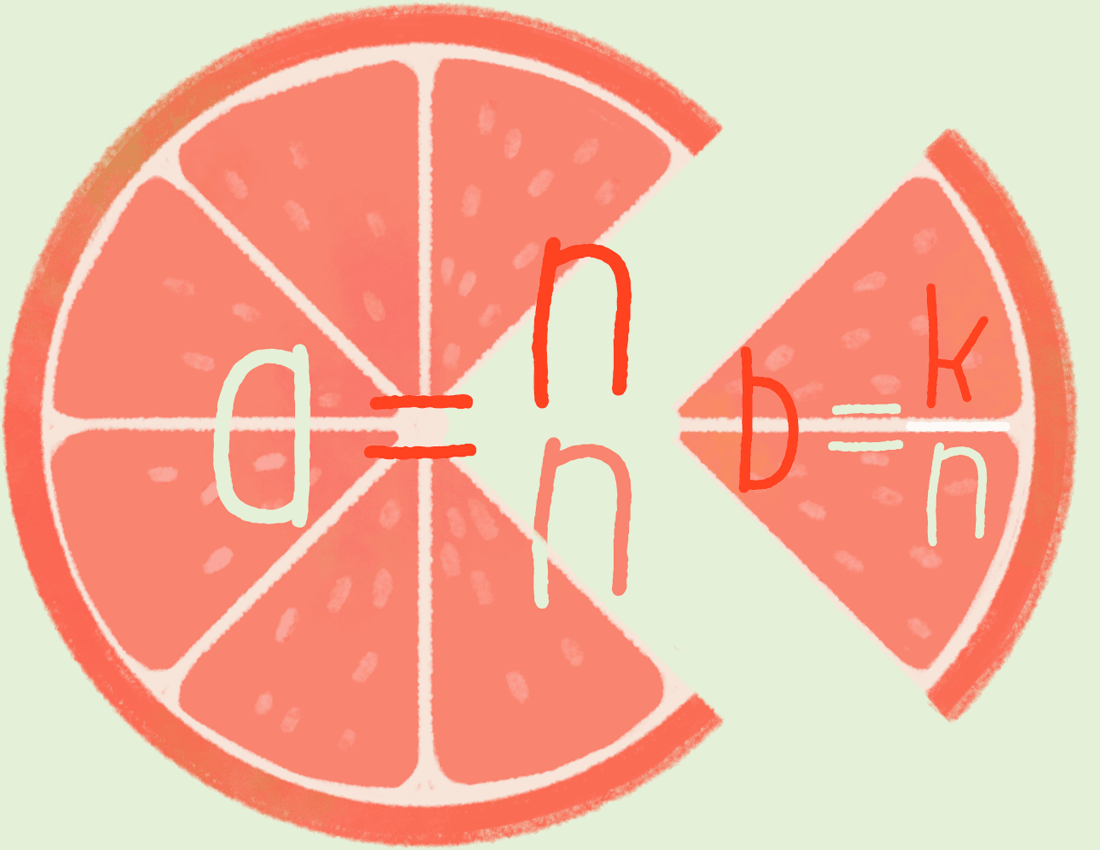
Приведение к общему знаменателю.

Отзывы:
Преподаватель:
Степан
Сегодня разобрали многое на занятии. Были затруднения при решении геометрических задач, но ребенок тему понял. Контрольную работу написал на 5
Преподаватель:
Ульяна
Очень позитивный настрой на занятиях. Хочется заниматься, ребёнок рад!
Преподаватель:
Андрей
Все очень понравилось. буду и дальше с радостью заниматься!


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход