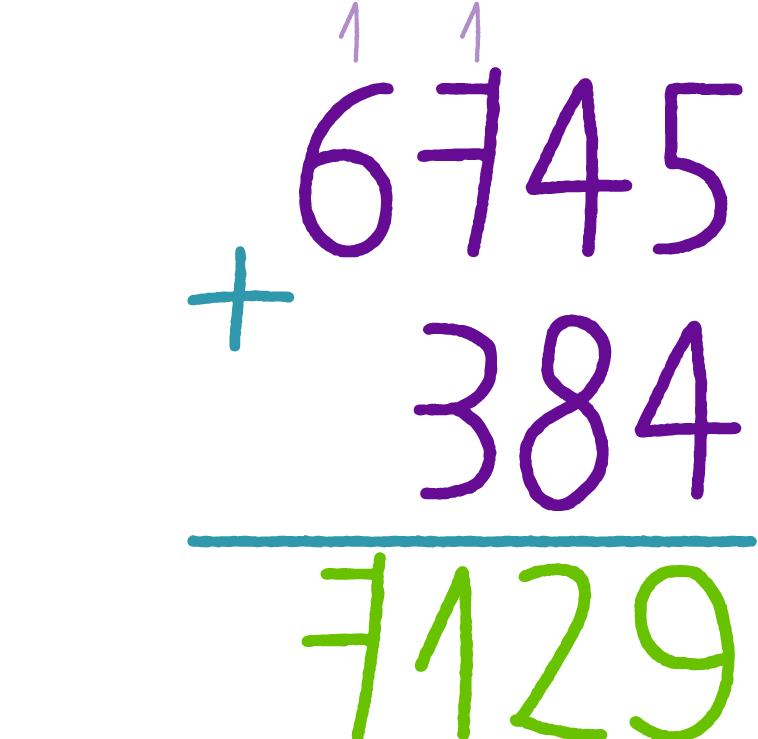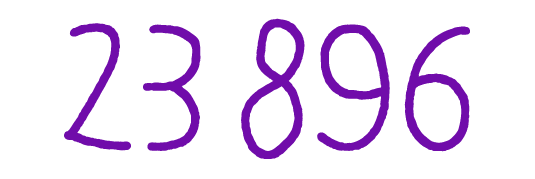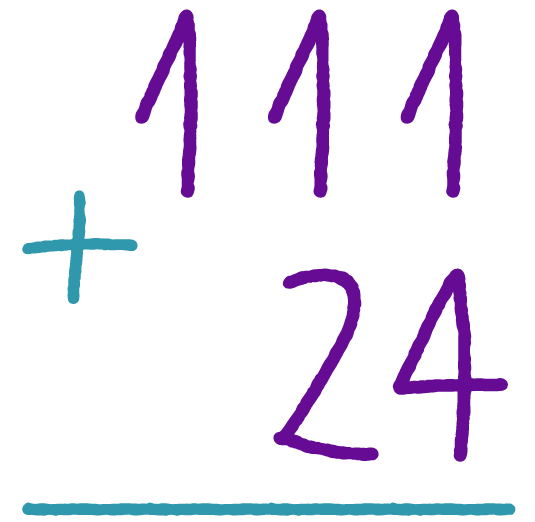Сложение натуральных чисел. - онлайн урок




Сложение натуральных чисел.

Отзывы:
Преподаватель:
Анастасия
Сегодня у меня была официальная онлайн конференция с педагогом моей дочери (она учится в 6 классе CAVA Academy- Конкорд, Калифорния, США), педагог рассказала мне о результатах теста по математике, Анастасия опередила своих одноклассников по баллам, вышла на уровень 7 класса. Это несомненно большая заслуга и труд Елены Анатольевны, низкий поклон. Анастасия всего второй год учится в США, поначалу ей было сложно освоить американскую методику преподавания. Благодаря Елене Анатольевне Анастасия уверенно решает сложные задачи и примеры, значительно улучшила скорость при решении. Одним словом, мы очень довольны и благодарны школе «Альфа» за то, что у нас есть Елене Анатольевна.
Преподаватель:
Тимур
Очень рада, что попали на данного преподавателя! Результат получен уже с 3 занятия, эффективные методы объяснения! В полном восторге)
Преподаватель:
Станислав
Хочу сказать вам спасибо за замечательного преподавателей по чтению! Стасик показывает успехи по предметам, прям рванул вперёд. Ему очень нравятся занятия, и то, что я слышу очень нравится и мне. Всегда увлекательно, с добротой, с большим терпением и вниманием! Это огромное счастье, что мы вас нашли


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход




.png)