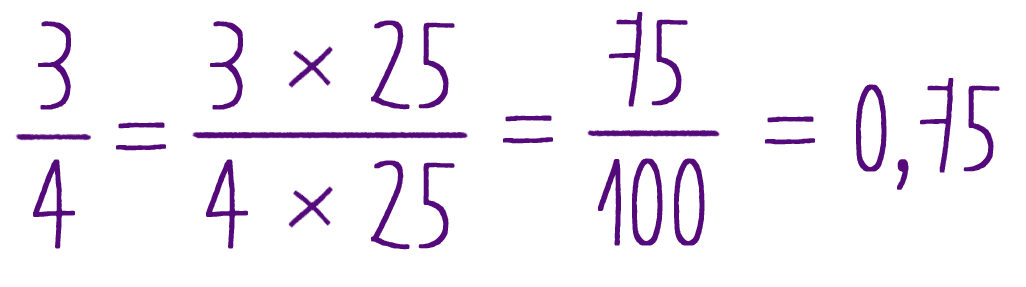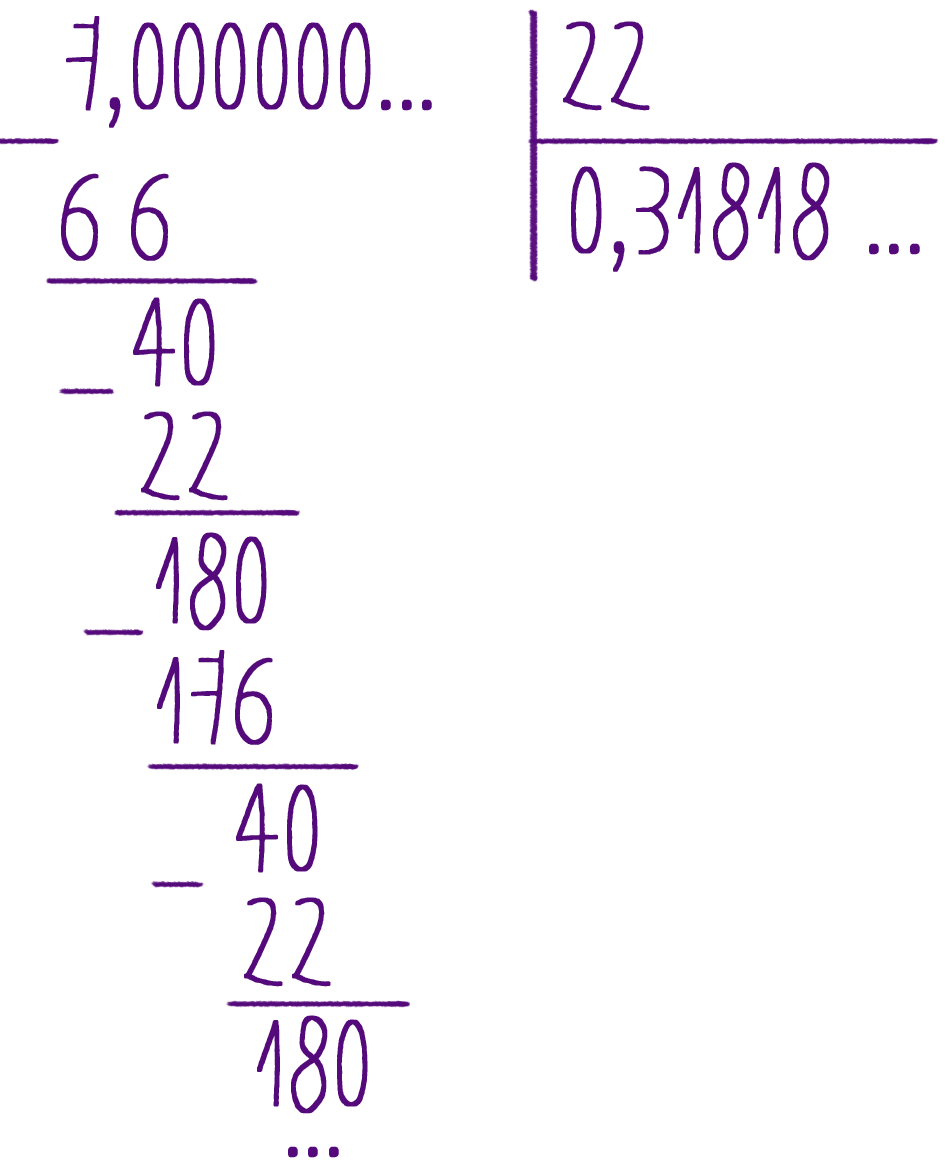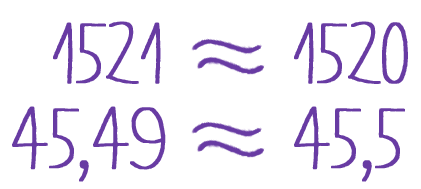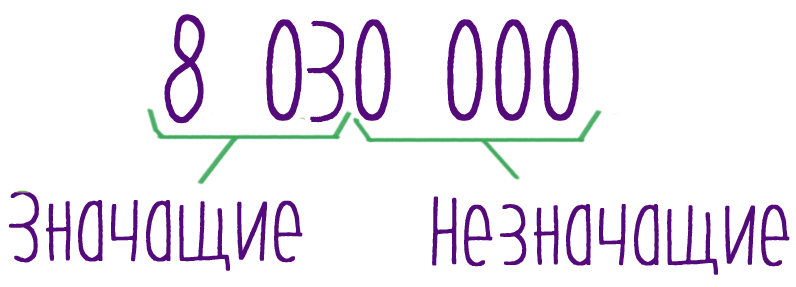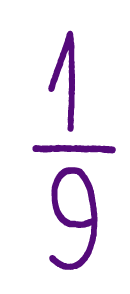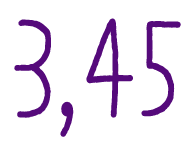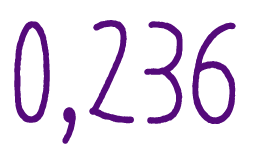Приближенные вычисления с действительными числами - онлайн урок

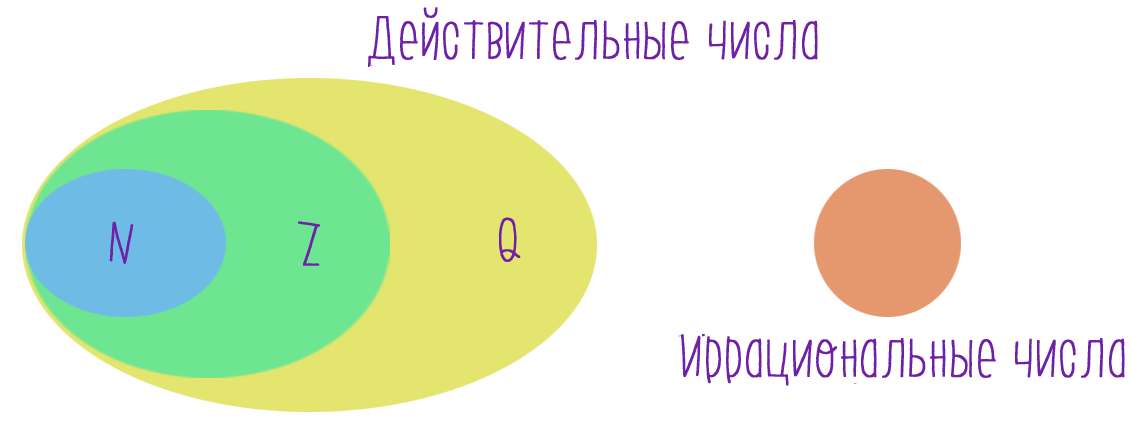
Приближенные вычисления с действительными числами

Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

Рациональные числа – это числа, которые можно записать в виде дроби mn, где m – целое, а n – натуральное число.

Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным (нерациональным) числом.

Рациональные и иррациональные числа называют действительные числа.

Если знаменатель q несократимой дроби pq не имеет других простых делителей, кроме 2 и 5, то эта дробь разлагается в конечную десятичную дробь.

Любое рациональное число разлагается в периодическую дробь, а любое иррациональное – в непериодическую дробь.

Правило округления:

Если первая отбрасываемая цифра меньше 5, то нужно округлять с недостатком, а если это цифра больше или равна 5, то нужно округлять с избытком.

Значащими цифрами числа называют его все цифры, кроме нулей, стоящих левее первой, отличной от нуля цифры, и нулей, стоящих в конце числа, если они взяты взамен неизвестных или отброшенных цифр.

Теперь установи соответствие между картинками и определениями, которые мы только что повторили.

Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:

1. Правила сложения и вычитания бесконечных десятичных дробей;

2. Правила умножения и деления бесконечных десятичных дробей.

Для продолжения урока кликните на кнопку ниже:

Отзывы:

Рафаэль

Замечательный педагог; выявил все пробелы; понятно и терпеливо объяснил все

Вячеслав

Спасибо за урок нашему учителю! Алексей Сергеевич - педагог очень вежливый, терпеливый, корректно и уважительно отнесся к моему ребёнку, проявил индивидуальный подход и понимание в пробелах ученика. Объясняет медленно и разборчиво, не торопит ребенка, провоцирует мыслить и рассуждать самостоятельно- что важно! Вячеслав сначала очень стеснялся и был настроен воинственно- так как не любит математику и с трудом понимает учителя в школе, в ходе урока у Славы появилось доверие к учителю и он не против продолжить обучение, мы, как родители этому очень рады

Юрий

Очень хорошая онлайн школа. Хорошо и понятно объясняют темы

Похожие уроки

Умножение многозначных чисел (п)

Проверка деления. Знакомство с калькулятором

Урок: "Тригонометрическая окружность"

Марафон нестандартных задач (#практика)