УРОК 93. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ СИНУС И КОСИНУС.

Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

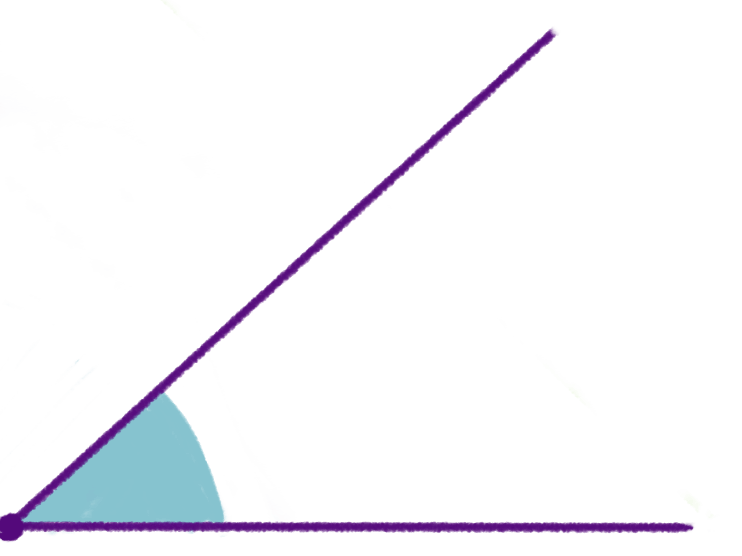
Острый угол — это угол от 0° до 90°.

Прямоугольный треугольник — это треугольник, в котором один из углов прямой, т.е. он равен 90°.

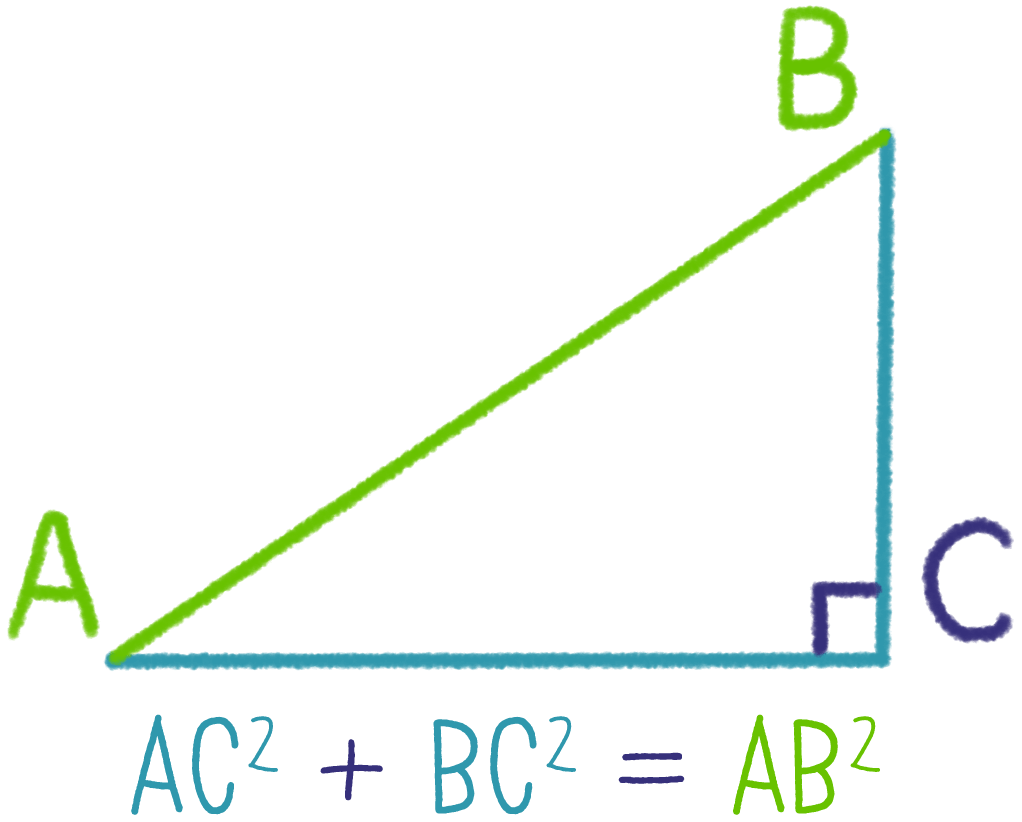
Теорема Пифагора: в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

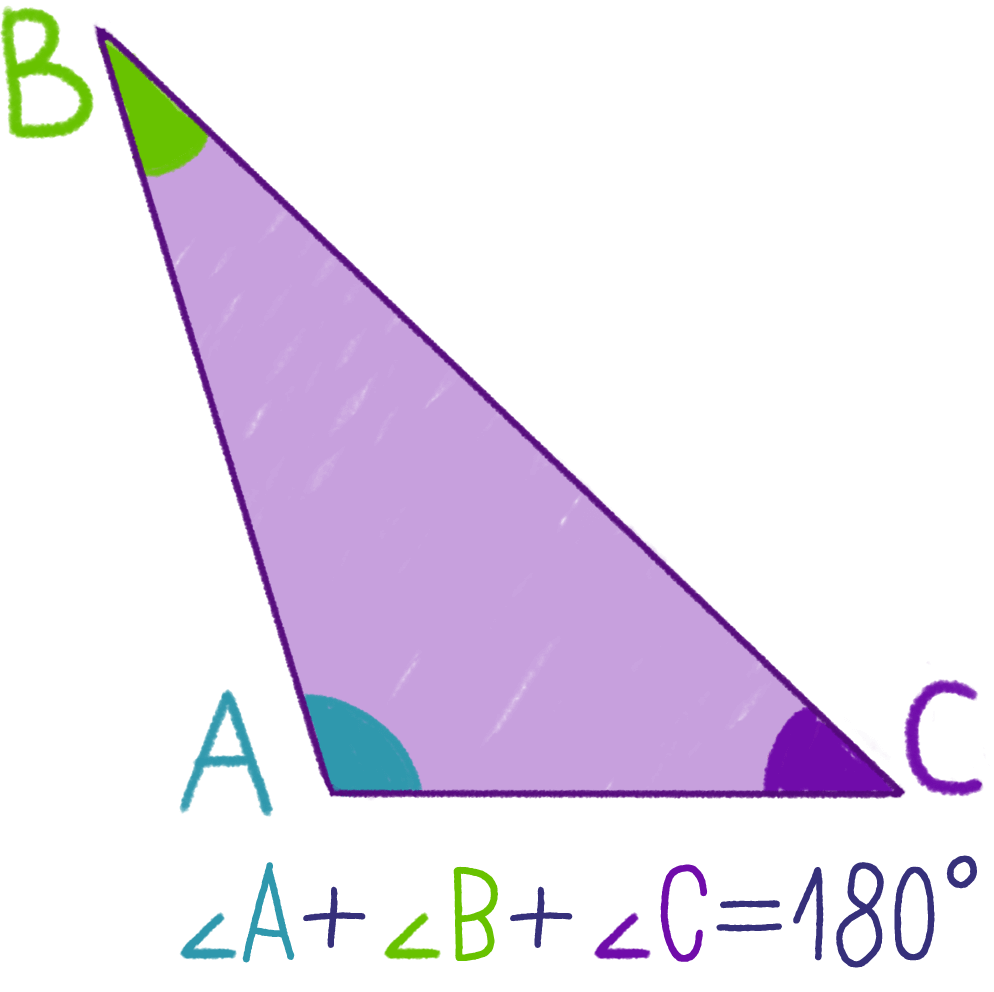
Сумма всех углов любого треугольника - величина постоянная и равна 180°.

Теперь выбери соответствия между картинками и определениями, которые мы только что повторили.

Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:

Тригонометрия.
Тригонометрические функции.
Синус острого угла.
Косинус острого угла.

В математике не всегда можно измерить длину при помощи линейки, например длину до Луны или Солнца. Также не всегда можно измерить угол при помощи транспортира.

А зачастую важно знать точное значение величин. В таких случаях используют треугольники.

Все вычисления, связанные с

выделяют в отдельный раздел - ТРИГОНОМЕТРИЯ.

Впервые термин "тригонометрия" упомянул в 1595 году немецкий математик Бартоломеус Питискус, хотя первые теоремы, которые относятся к тригонометрии, были озвучены еще в IV веке до нашей эры.

Тригонометрия – в буквальном переводе означает измерение треугольников (от др.-греч. «треугольник» и «измеряю»). В данном случае это следует понимать, как решение треугольника, т.е. определение его сторон, и других элементов.

В были найдены все зависимости между сторонами и углами треугольников, были получены соответствующие формулы.

Итак, тригонометрия начинается с прямоугольного треугольника — любой треугольник можно разбить на

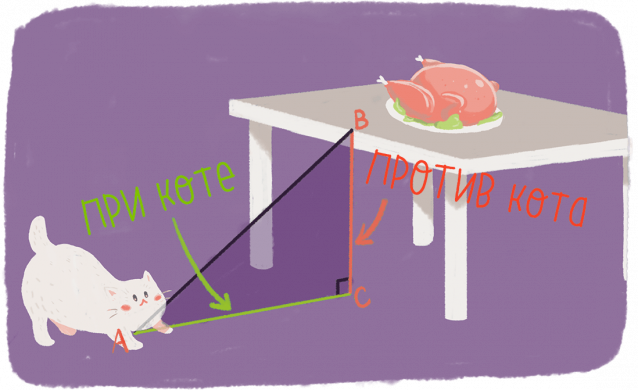
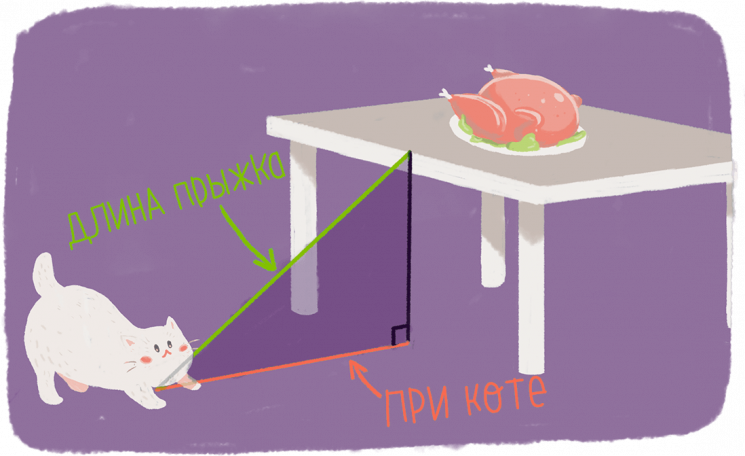
Например, кот хочет съесть курицу, которую случайно оставили на столе. Для этого ему нужно запрыгнуть на стол. Согласитесь, не совсем простая задача, т.к. нужно правильно найти лучшее расстояние, с которого можно сделать прыжок, не забыть про высоту стола и т.п.

Первое, с чего стоит начать – это найти в этой задаче треугольник!

Пусть

– прямоугольный треугольник с прямым углом С.

Тогда:

• АВ –

;

• BC и

– катеты;

• ∠А и ∠

– острые углы;

• ∠С =

°.

Тригонометрические функции – это элементарные функции, которые возникают при рассмотрении прямоугольного треугольника и выражают зависимость между сторонами и углами треугольника. Всего основных тригонометрических функций четыре: синус, косинус, тангенс и котангенс.

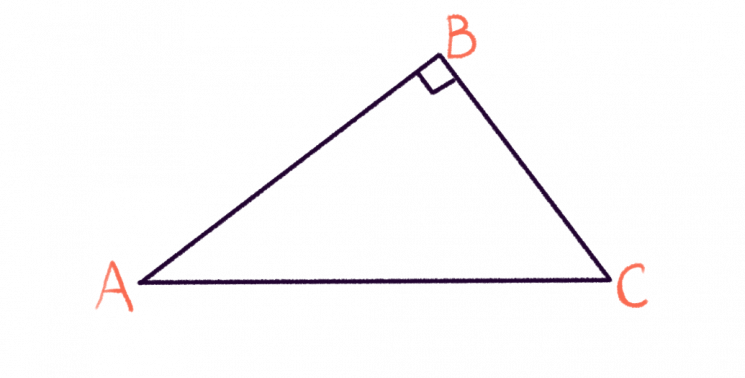
Вернемся к △АВС и обозначим его углы:

∠

= α;

∠

= β;

∠АСB =

°.

Введем определение первой функции.

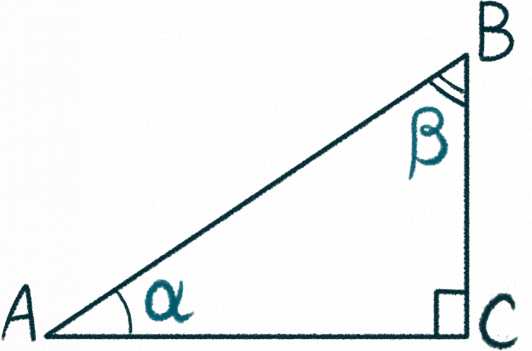
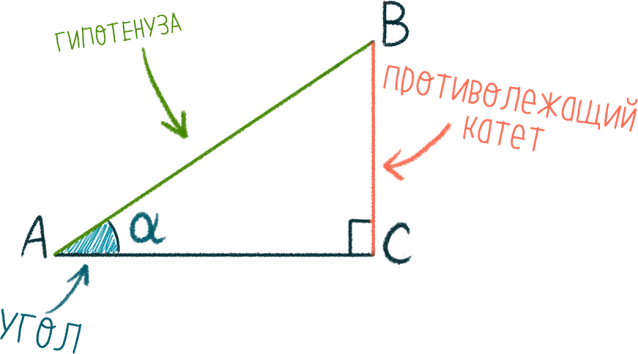
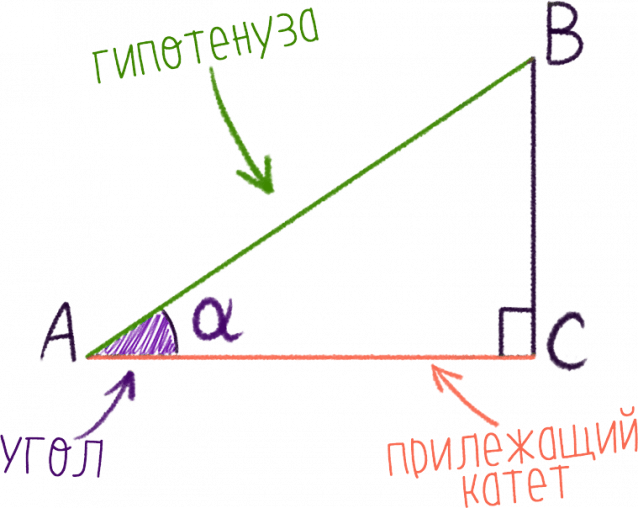
Синусом острого угла прямоугольного треугольника называют отношение противолежащего ему катета к гипотенузе.

В нашем случае:

sin(α) = AB .

Функция синус от некоторого угла α обозначается как sin(α). В результате ее применения всегда получаем

Чтобы запомнить определение синуса, можешь вспомнить кота, который хочет запрыгнуть на стол.

Синус – это высота стола (ПРОТИВ кота – ПРОТИВолежащий катет), деленная на длину прыжка (

Задача. Дан треугольник АВС с прямым углом В. Найдите синус угла А этого треугольника, если АВ = 8, BС = 6, АС = 10.

Попробуй решить задачу самостоятельно и проверь ответ.

Ответ: sin(∠A)=

Решение.

В треугольнике АВС относительно угла

— гипотенуза;

— противолежащий катет.

По определению синуса острого ∠А треугольника АВС:

sin(∠A) = BC =

= 10 = 3/5 =

= .

Ответ: sin(∠A) =

Рассмотрим обратную задачу. Пусть дан треугольник АВС с прямым углом С. И, например, sin(∠A) = 5/13.

Запишем синус угла А по определению:

sin(∠A) = AВ .

С другой стороны, по условию:

sin(∠A) = ВС AВ = 5 .

Это означает, что стороны ВС и АВ соотносятся как 5 : 13. Поэтому, для простоты вычислений, примем ВС = 5. Тогда:

АВ = .

Запишем теорему Пифагора для треугольника:

AB² =

² + BC².

Откуда:

= √AB² - BC² =

= √13² - ² =

Нарисуем полученный треугольник в тетради:

1) рисуем

треугольника по пересекающимся под прямым углом клеточкам в тетради;

2) обозначаем

треугольника;

3) проводим

∠A - искомый угол!

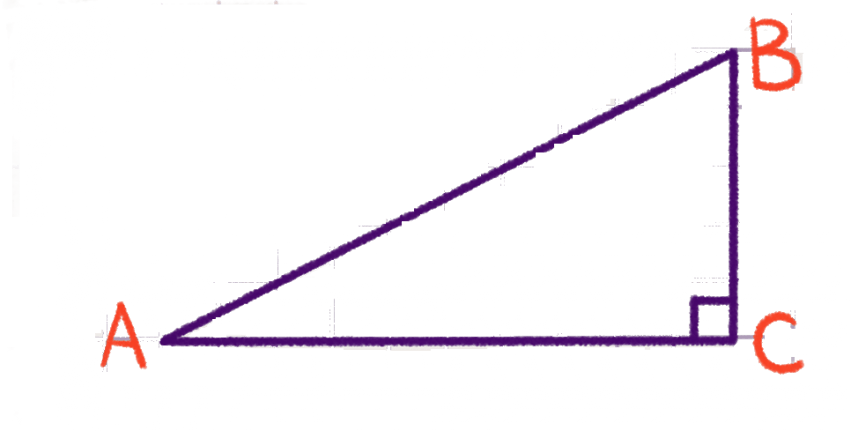
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего к этому углу катета к гипотенузе.

В случае нашего треугольника:

cos(α) = AB .

Чтобы запомнить определение

, можешь вспомнить кота, который хочет запрыгнуть на стол.

Косинус – это длина до стола (ПРИ коте –

катет ) деленная на длину прыжка (гипотенуза).

Задача. Вычислить cos(45°).

Попробуй решить задачу самостоятельно и проверь ответ.

Ответ: cos(45°) = √2 .

Решение.

Рассмотрим прямоугольный треугольник АВС, один из углов которого равен 45°:

∠C = 90°;

∠B =

°.

Найдем третий угол по теореме о

углов треугольника:

∠А + ∠B + ∠С =

°.

∠А = 180° - ∠B - ∠

∠А = 180° -

° - 90° = 45°.

Значит, треугольник АВС -

: его катеты равны.

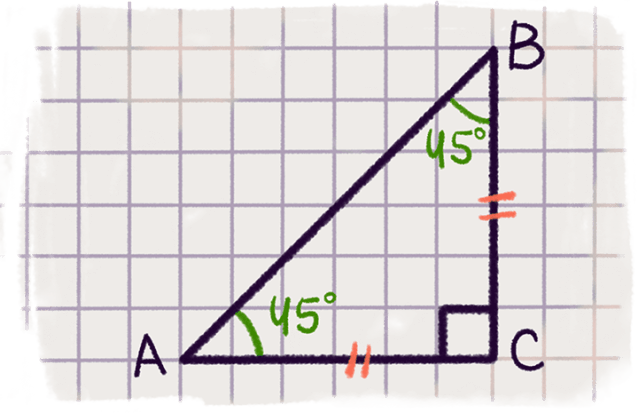
Без потери общности, будем считать, что его катеты равны единице:

AC = BC =

Неизвестную длину гипотенузы найдем по теореме Пифагора:

АВ = √BC² + AC² = √ ² + 1² = √2.

Теперь найдем косинус одного из острых углов:

cos(∠A) = cos(45°) = AC =

= √2 =

= √2 .

Ответ: cos(45°) = √2 .

На нашем первом уроке по тригонометрии мы познакомились с тобой с тригонометрическими функциями синуса и косинуса, научились решать задачи, используя эти определения.

Теперь наш кот сможет вычислить точный угол, под которым ему нужно будет выполнить прыжок на стол за курицей.

Дан прямоугольный треугольник АВС с прямым углом В. Найдите косинус угла А этого треугольника, если АВ = 8, BС = 6, АС = 10.
Дан прямоугольный треугольник АВС с прямым углом С. Также cos(∠A) = 0,2. Нужно построить угол А.
Вычислить sin(30°), используя равносторонний треугольник.
Докажите cos(90° − α) = sin(α), используя определения тригонометрических функций.
Упростить выражение 2sin²(α) + cos²(α) − 1, используя определения тригонометрических функций.